- Description of the algorithm Read the source data Merging lists File merging
- Evaluation algorithm
- Strengths and weaknesses
- Implementation
- Development
- References
- External links
|class=Sorting algorithm
|image= Funnel_sorting_algorithm_with_merging.gif
|caption=Static visualization of funnel sort Пример сортировки воронкой. Каждый входящий элемент либо добавляется в начало/конец существующих упорядоченных подмассивов, либо сам образует начало нового подмассива.
|data=Array
|time=
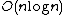
|best-time=
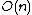
|average-time=
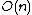
|memory=
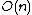
|optimal=No
|space=
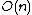 total
total  auxiliary
auxiliary}}
Funnel Sort is one of the fastest known universal data sorting algorithms. It requires a once allocated temporary memory buffer equal to the sorted array (which is represented in RAM in the form of a list) and has no recursions. If the amount of RAM is insufficient, automatically switches to the "external sorting" mode, that is, splits the original data into several sequences (depending on the amount of available RAM), and then merges the sorted temporary files into the resulting one.
The algorithm was proposed by Vladimir Rybinkin on January 9, 2019 on [https://www.facebook.com/vladimir.rybinkin/posts/2162529770534652 on his page in Facebook].
Description of the algorithm
Funnel sorting is a significantly improved version of the Merge sorting algorithm. The principal difference is that sorted data arrays for a merge are formed dynamically, and their size is determined by the sequence of input data itself. In particular, if the array is already sorted (in direct or reverse order - it almost doesn’t matter), immediately after the data is loaded into RAM, they will already be organized as a fully sorted single list, which can only be sent to the output stream.
Read the source data
A funnel is a collection of k ordered lists (initially empty). To minimize the number of comparisons, the current input element, regardless of the number of elements in the list, is compared only with the head and tail of the corresponding list: if it is less than or equal to the first element, it becomes its head, if it is greater than or equal to the last element, it is added to the tail. If neither the one nor the other, it goes to the comparison with the head and tail of the next list (if there is one) or forms the next list itself, being in it the head and the tail simultaneously. Thus, the elements of these lists form a “funnel”: the head of each following list is guaranteed to be larger than the head of the previous one, and its tail, respectively, is smaller. Therefore, when moving along the “funnel”, the probability that the next element will be attached somewhere without increasing the size of the funnel is rather high.
The elements of the input stream are placed in the RAM, which is also ordered dynamically, in blocks of at least the maximum size of the element (usually much larger), once the ordered RAM has been exhausted. Each element is preceded by a passport of the form "element size in bytes" (determined when reading the element) and "address of the next element" (initially zeroed out), that is, the input data stream is converted into a list. Such an organization of data allows sorting without moving the elements themselves and provides an economical use of memory to store non-uniform data (usually, these are lines that may vary thousands of times in length), and only the amount required for this particular element is allocated for each of them.
Merging lists
The need to merge lists arises if:
- the element cannot be attached to the funnel (all k of the funnel lists are full);
- input stream exhausted (all data is loaded into RAM);
- exhausted available RAM (there is no place to place the next element).
The merging algorithm of ordered arrays is well known: at each step, the smaller of the current elements of the subarrays is taken and sent to the resulting array. The counters of the numbers of the elements of the resulting array and the subarray from which the element was taken are increased by one. When one of the subarrays is over, the remaining elements of the second subarray are added to the resulting array. Since arrays in RAM are presented as lists, the merging of two subarrays occurs without moving the data elements themselves, which is much faster.
The mechanism for merging lists when an overflow funnel can be implemented, for example, as follows: the two smallest (by volume or by number of elements) lists merge into one - into the one that takes the place of the older one by the funnel of the merged list (in this case the funnel remains a funnel the head and tail of any list are guaranteed to be within the range of any of the higher lists and outside the range of any of the lower ones, all the lists are smaller than the youngest of the merged ones are shifted by one, and the last list of the funnel is reset.
If the input data stream or available RAM is exhausted, all the lists are first merged into pairs in pairs, starting with the smallest ones, and then this list is sent to the output stream. The sorting process is complete.
File merging
This step is performed only if there is a shortage of RAM to accommodate the entire data array being sorted. The temporary files are merged into a new file with the subsequent deletion of two merged files, until the temporary files are completely exhausted. The merge algorithm is the same as when merging lists.
Evaluation algorithm
The funnel sorting algorithm belongs to the class of algorithms based on the comparison of elements. They are flexible in application, but have a fundamental performance limit for the worst case: it cannot be better than O (n * log2n). The worst case for this algorithm is well known: if the input stream is also sorted by a “funnel” and does not have identical elements, i.e. a) the minimum element b) the maximum c) the minimum of the remaining d) the maximum of the remaining (for example, when sorting numbers: 1, 99, 2, 98, 3, 97, ...), etc. In this case, only two elements fit into the funnel array, and the algorithm is actually reduced to the classical merge sorting algorithm, in which the first step is combined with the process of reading elements into RAM. As you know, this algorithm has exactly the complexity of O (n * log2n) - both for the worst case and for the best. Practice, however, shows that in the real world, sortable data sets often contain ordered subarrays, and any ascending or descending subsequence is guaranteed to be “caught” by a funnel the size of even one list! Therefore, the funnel sorting for the best case (when the input data is already sorted) will be performed in linear time O (n).
The average complexity with a random distribution of input data can only be estimated as probabilistic. Obviously, the more monotonically increasing or decreasing subsequences in the source data, the more repeated elements there are, the sorting time will be more “linear” - especially if we take into account the loading times of the source data and the recording of results. Moreover, when reading and writing data, access to them is consistent, that is, as fast as possible. Experiments have shown that the sorting time is comparable with the time of copying files or any other linear data processing. Testing on specially prepared arrays for the best and worst case with a volume from a million to one hundred million lines showed: despite the fact that the number of comparisons of elements differs by orders of magnitude, the total sorting time slows down only by tens of percent (in all experiments less than twice) . For comparison: the lack of RAM due to a sharp increase in the number of file operations slows down the sorting time tenfold.
Strengths and weaknesses
Advantages:
- One of the fastest (in practice) of the general-purpose internal and external sorting algorithms.- Universal. Sorts practically any data types - in particular, arrays with elements of constant or variable length.- Stream processing of input data: if for other algorithms it is required to preload the entire data array into RAM, after which the actual sorting begins, then the funnel has almost finished it.- Behavioral behavior: when processing already ordered or partially ordered data, the sorting time is noticeably reduced.- Works in conditions of limited resources (lack of RAM).- Works on sequential access data structures.- Does not have "difficult" input data.- Easy to implement.- Requires only O (n) additional memory for its work.Disadvantages:
- Unstable.Generally speaking, the stability of the algorithm is not a problem if all the keys are different (it depends on the input data) or when identical elements are indistinguishable - for example, when the entire element is a key (this is exactly how the element comparison algorithm in this implementation is arranged). In extreme cases, the algorithm can be easily refined to ensure stable sorting by expanding the key with the initial index of the element in the array. In the case of equality of the main keys, the comparison is made according to the index, thus excluding the possibility of changing the relative position of equal elements. This modification requires additional memory in the size of the index for each element, which is initialized by the value at the time of reading the array in RAM.
Implementation
The most obvious improvement in the algorithm is to separate the processes of filling the funnel lists and merging them, as well as determine the optimal size of the funnel itself: as the maximum number of lists increases, the time for searching for a place to place the next element increases, albeit slightly. slow down the process of merging lists - after all, they can be from two elements to many thousands and even millions! Experiments have shown that the size of the funnel has almost no effect on efficiency (the funnels were tested in 1, 2, 4, 8, ... 64 lists): the increase in time to add an item is almost offset by a decrease in the number of mergers of larger lists. Therefore, the simplest version was implemented with the size of a funnel in one list, requiring no more than two comparisons for the extension of an element. But the size of the buffer of sorted lists before the merge, on the contrary, was chosen sufficiently large (1024 lists), with overflow of which three-fourths of the smallest lists of this buffer (up to 256) merge at once. This technology allows you to effectively sort failed (close to the worst case) source data sets, combining large arrays just before writing the results to a file.
Optimizing the process of merging temporary files is not very relevant and noticeable only when there is a serious lack of RAM, when the number of cuts to files and subsequent merges reaches hundreds or even thousands - for example, when sorting gigabyte files with a utility compiled for MS-DOS with 300-400 RAM available kilobyte But even in this case, the sorting is quite confident and not very long. The maximum number of files is defined in 36 (numbers and letters of the Latin alphabet) with a collapse at overflow up to 16 at once.
Development
The funnel sorting algorithm (as well as other algorithms based on comparisons) has quite a good potential for increasing functionality. In the current implementation, sorting is carried out by increasing the value of the data byte in the string - the most versatile comparison mechanism that allows you to sort texts in different languages and data structures that contain non-text characters. But, ideally, the method of comparing elements should be customizable by the user (or generally user). In particular, it is possible to provide the possibility of sorting in ascending or descending order, alphabetically Russian (in encodings WIN-DOS-KOI-UTF et cetera), Arabic, Chinese and other languages, with or without ignoring the case of characters, sorting data of different types (integer , real, date, time), sorting by fields of tables and other structures, the ability to override the terminator value (by default - the line feed character 0x0A) or the array length (when sorting data structures of constant length), etc. In any case, only the procedure for comparing elements is set up - the rest of the sorting algorithm “funnel” remains unchanged.
References
External links
- Description of the algorithm on the author's website (rus.)
- About the author (rus.)
- Otfrid Foerster
- Otfried
- Otfried Mueller
- Otfried Muller
- Otfried Nippold
- Otfried Preussler
- Otfried Preußler
- OTFT
- OTG
- Otha D. Wearin
- Othala
- Othala Rune
- Othar Turner
- Otha Turner
- Otha Wearin
- Othaya
- OTH-B
- OTH-B Radar
- Othea
- Othella Harrington
- Othello
- Othello (1951 film)
- Othello (1965 British film)
- Othello board games
- Othello list of characters