“Draft:Semisimple representation”的意思、由来-开放百科全书

词条

Draft:Semisimple representation

释义

Equivalent characterizations
Proof of equivalences
References

In mathematics, a semisimple is a representation that is a direct sum of simple representations.

Equivalent characterizations

Let V be a representation of a group G. Then the following are equivalent:

V is semisimple as a representation.
V is a sum of simple subrepresentations.
Each subrepresentation W of V admits a complementary representation: there is some subrepresentation W{{'}} such that .

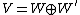Proof of equivalences

A proof here is based on the next Lemma, which is of independent interest:

{{math_theorem||name=Lemma|math_statement=Let p:V → W be a surjective equivariant map. If W is semisimple, then p splits; i.e., it admits a section.}}

Assuming the lemma for a moment, we can give the proof.

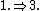: Take p to be the natural map . Since V is semisimple, p admits has a section 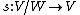and so .

: This direction is by transfinite induction:

References

{{Fulton-Harris}}

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。