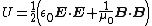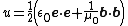- Time-reversal waves Conjugate transform Time reversal transform Time reversal Maxwell equations Time reversal signal processing
- Background of time-reversal wave Action at a distance Absorber theory Transactional interpretation for quantum mechanics Welch's reciprocity theorem Rumsey's reciprocity theorem Inner product space for the electromagnetic fields on a closed Surface Zhao's mutual energy theorem de Hoop's reciprocity theorem The forgot second Lorentz reciprocity theorem
- Some property of time-reversal wave Poynting theorem of the time-reversal wave Time-reversal wave can balance out or cancel the energy of the normal wave
The waves satisfy time-reversal Maxwell equations are time reversal waves. There are two kind of time-reversal waves. One is the time-reversal wave corresponding to the retarded wave, another is the time-reversal wave corresponding to the advanced wave.
Here, the time-reversal wave is a possible physical wave exist in the nature. It satisfy time-reversal Maxwell equations.
Time-reversal waves
We know that Maxwell equations has two kind solution, retarded solution and advanced solution. Corresponding to the retarded solution there is the retarded wave. Corresponding to the advanced solution there is advanced wave. Advanced wave do not satisfy our traditional causality. Many people think the advanced wave are not real wave. But there are a few very famous physics believe the advanced wave exist. Assume the retarded wave and advanced wave all exist. The question is that is the advanced wave the time-reversal wave of the retarded wave? The answer is negative. Maxwell equations are not time-reversible. We can define the time-reversal waves for the retarded wave and define the time-reversal wave for the advanced wave. The question is the time-reversal waves exist or not?
Conjugate transform
It is not clear who first introduced the concept of the conjugate transform, but the details theory of the conjugate transform can be found in
({{lang|en|Jin Au Kong}})[1]. The conjugate transform can be seen in following,

or
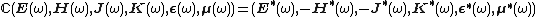
Where
 is the conjugate transform.
is the conjugate transform. 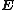 is electric field.
is electric field.  Magnetic field.
Magnetic field.  current intensity.
current intensity.  magnetic current intensity.
magnetic current intensity.  is permittivity,
is permittivity, 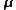 is permeability,
is permeability,  is time,
is time, 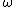 is frequency.
is frequency.
It is important that if a field satisfies the Maxwell equations, after the conjugate transform,
it still satisfies the Maxwell equations. If the original field is retarded wave, after the transform it becomes advanced wave. Vice Versa, if the original field is advanced wave, after the transform it becomes the retarded wave.
Time reversal transform
Time reversal transform is different with conjugate transform. It can be defined as following
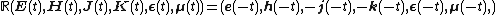
or
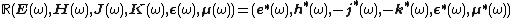
Where 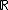 is time reversal transform.
is time reversal transform. 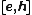 is the time-reversal electromagnetic field.
is the time-reversal electromagnetic field. 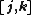 is time-reversal electric current intensity and time-reversal magnetic current intensity. After the time-reversal transform
is time-reversal electric current intensity and time-reversal magnetic current intensity. After the time-reversal transform 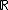 , a normal electromagnetic field become time-reversal magnetic fields. The time-reversal electromagnetic fields do not satisfy Maxwell equations, but they satisfy time-reversal Maxwell equations.
, a normal electromagnetic field become time-reversal magnetic fields. The time-reversal electromagnetic fields do not satisfy Maxwell equations, but they satisfy time-reversal Maxwell equations.
Assume there is a retarded wave, the time-reversal wave corresponding to this retarded wave is not the advanced wave. The advanced wave is from current time go to the past time. The time reversal wave is from a future time go to the current time. Advanced wave still satisfy Maxwell equations, it is a normal electric field. Time-reversal wave does not satisfy Maxwell equations, it is not a normal electromagnetic field.
Time reversal Maxwell equations
| Name | Integral equations | Differential equations | Meaning | ||
|---|---|---|---|---|---|
| time-reversal Gauss's law | {{oiint | intsubscpt=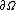 | integrand=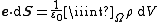 | 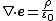 | The electric flux through a closed surface is proportional to the charge inside an enclosed volume. |
| time-reversal Gauss's law for magnetism | {{oiint | intsubscpt = 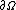 | integrand = 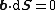 | 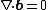 | The magnetic flux through a closed surface is zero (i.e. there are no magnetic monopoles) |
| time-reversal Maxwell–Faraday equation (Faraday's law of induction) | 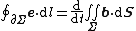 | 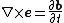 | The work per unit charge required to move a charge around a closed loop equals the rate of decrease of the magnetic flux through an enclosed surface. | ||
| time-reversal Ampère's circuital law (with Maxwell's addition) | 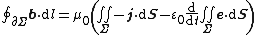 | 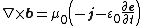 | The magnetic field induced around a closed loop is proportional to the electric current plus displacement current (proportional to the rate of change of electric flux) through an enclosed surface. |
Time reversal signal processing
It is worth to say that there is also a kind technology is referred as time-reversal focus method, which is applied normal electromagnetic field to simulate some property of time-reversal waves, please see Time reversal signal processing for details. Here the time-reversal wave doesn't mean that kind of technology.
Background of time-reversal wave
Here some thing related the time-reversal wave will be discussed. Perhaps the time-reversal wave Alberta doesn't involve.
Action at a distance
The theory of action-at-a-distance are introduced by
({{lang|en|K. Schwarzschild}})[2]
({{lang|en|H. Tetrode}})[3]
({{lang|en|A.D. Fokker}})[4].
According to this theory, an electric current will produce two electromagnetic potentials or two electromagnetic waves: one is the retarded wave, another is advanced wave. The emitter can send the retarded wave, but in the same time it also sends an advanced wave. The absorber can send the advanced wave, but in the same time it also sends a retarded wave. According to this theory, the sun cannot send the radiation wave out, if it stayed alone in the empty space. Infinite absorbers are the reason that the sun can radiate its light. The action can be written as following,
{{Equation box 1|indent =:
|equation =
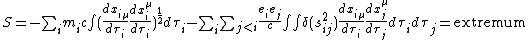
|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
where
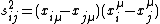
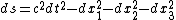
Absorber theory
The absorber theory is introduced by Wheeler and Feynman
({{lang|en|J. A. Wheeler}})[5]
({{lang|en|J. A. Wheeler}}).[6]
The absorber theory is build on the top of the above theory of the action-at-a-distance
({{lang|en|A.D. Fokker}})[4]
({{lang|en|K. Schwarzschild}})[2]
({{lang|en|H. Tetrode}})[3]
. A cording to this theory, electromagnetic field has no its own freedom. The electromagnetic field is adjective field. It is only a bookkeeper for the action or reaction between at least two charges. That means without a test charge or absorber, only the emitter alone can not produce the radiation. Absorber theory try to offer a better explanation to the recoil force of an accelerated or decelerated charge in empty space. The recoil force has been introduced by Dirac
({{lang|en|P. A. M. Dirac}})[7].
But Wheeler and Feynman do not satisfy that Dirac did not offer a reasonable reason of that formula. Wheeler and Feynman try to use the absorbers stayed on the infinite big sphere to explain the formula given by Dirac. The absorber theory also emphases the importance of the absorber in the radiation process.
Transactional interpretation for quantum mechanics
The transactional interpretation of quantum mechanics introduced by John Cramer
({{lang|en|John Cramer}}).[8]
The transactional interpretation is build on the top of Wheeler–Feynman absorber theory. In this theory, the emitter can send an offer wave to the absorber, when the absorber receive the offering wave, it can send a confirmation wave to the emitter. These two waves can have a handshake. This handshake process is the transactional process. In this process the photon or other particle is produced. The confirmation wave is advanced wave.
Welch's reciprocity theorem
This theory is introduced by W. J. Welch proposed in 1960
({{lang|en|W. J. Welch}}).[9] The theorem can be seen in the following,
{{Equation box 1|indent =:
|equation =
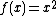
|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
In order to prove the above formula, it is required to prove a surface integral vanishes. The surface is on the infinite big sphere.
The proof of the vanish of the surface integral on infinite big sphere need the two waves one is retarded wave and another is advanced wave.
Rumsey's reciprocity theorem
V.H. Rumsey has introduced his summarize the Lorentz reciprocity theorem as "action and reaction". He has apply the complex conjugate transform to his "action and reaction" theorem and obtained a new reciprocity theorem
({{lang|en|V.H. Rumsey}}),[10]
{{Equation box 1|indent =:
|equation =
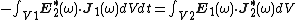
|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
Inner product space for the electromagnetic fields on a closed Surface
Shuang-ren Zhao has defined the inner product for any two electromagnetic fields which are ({{lang|en|Shuang-ren Zhao}})[14],
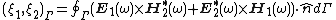
where 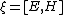 ,
, 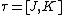 , Shuang-ren Zhao has proved that
, Shuang-ren Zhao has proved that
the above inner products, satisfy the Inner product space 3 definitions. If 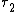 is taken as a unit vector of ether current
is taken as a unit vector of ether current 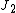 or
or 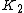 , the field
, the field 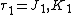 .
.
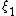 can be calculated ether on the original source
can be calculated ether on the original source 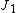 or on the surface
or on the surface  .
.  is any surface outside the two volumes
is any surface outside the two volumes  and
and  .
.
 is a unit surface normal vector. Shuang-ren Zhao has proved that this kind of
is a unit surface normal vector. Shuang-ren Zhao has proved that this kind of
inner product satisfy inner product space 3 conditions.
Zhao's mutual energy theorem
Shuang-ren Zhao has introduced the mutual energy theorem ({{lang|en|Shuang-ren Zhao}})[11]
in early of 1987.
Shuang-ren Zhao emphases that the mutual energy theorem is an energy theorem instead of some kind of reciprocity theorem. The theorem described an energy in the space.
{{Equation box 1|indent =:
|equation =
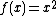
|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
where
 is any close surface or infinite big surface separating
is any close surface or infinite big surface separating  and
and  . We take the direction of
. We take the direction of  is from
is from  to
to  .
.
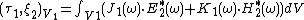
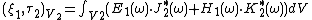
de Hoop's reciprocity theorem
Adrianus T. de Hoop published the time-domain cross-correlation reciprocity theorem in the end of 1987
({{lang|en|Adrianus T. de Hoop}})[12] which can be seen as following,
{{Equation box 1|indent =:
|equation =
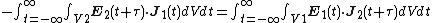
|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
The forgot second Lorentz reciprocity theorem
I. V. Petrusenko introduced the forgot second Lorentz reciprocity theorem in 2009
({{lang|en|I. V. Petrusenko}})[13].
It is similar to the Rumsey's reciprocity theorem or Zhao's mutual energy theorem.
Some property of time-reversal wave
Poynting theorem of the time-reversal wave
Apply time-reversal transform to the Poynting theorem,
{{Equation box 1|indent =:
|equation =
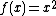
|cellpadding
|border
|border colour = #50C878
|background colour = #ECFCF4}}
where
we can obtained the Poynting theorem for time-reversal wave, which is in the following,
{{Equation box 1|indent =:
|equation =
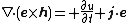
|cellpadding
|border
|border colour = #50C878
|background colour = #ECFCF4}}
Time-reversal wave can balance out or cancel the energy of the normal wave
Here the normal wave are the retarded wave and the advanced wave which satisfy Maxwell equations. The normal wave for example the retarded wave can be canceled or balanced out by the time-reversal wave corresponding to retarded wave. Similarly, the advanced wave can be canceled or balanced out by the time-reversal wave corresponding to the advanced wave.
If the time-reversal wave exist it can balance out the normal electromagnetic fields which means it is possible that,
{{Equation box 1|indent =:
|equation =
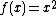
|cellpadding
|border
|border colour = #50C878
|background colour = #ECFCF4}}{{Equation box 1
|indent =:
|equation =
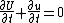
|cellpadding
|border
|border colour = #50C878
|background colour = #ECFCF4}}{{Equation box 1
|indent =:
|equation =
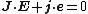
|cellpadding
|border
|border colour = #50C878
|background colour = #ECFCF4}}
Hence if time-reversal wave exist, and if they exist together with the normal waves. That will make the normal wave not carry energy.
In quantum physics, the waves are probability wave. A probability wave cannot carry energy. In order to make the wave not carry energy the time-reversal wave is required.
- Jim Risch
- Jim River
- Jim Rivera
- Jim Robinson
- Jim Robinson (trombonist)
- Jim Rockford (television character)
- Jim Rodford
- Jim Rodgers (finance)
- Jim Rogers
- Jim Rome
- Jim Rondeau
- Jim Ronny Andersen
- Jim Ronson
- Jim Rose Circus
- Jim Rosenfield
- Jim Ross
- Jim Ross Lightfoot
- Jim Roszko
- Jim Royle
- Jim Russell (cartoonist)
- Jim Ryan
- Jim Ryun
- Jim Sanborn
- Jim Sasser
- Jim Sauter