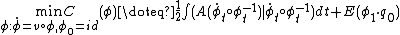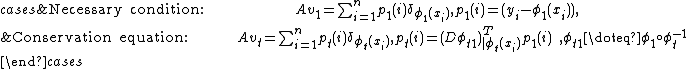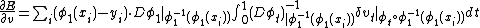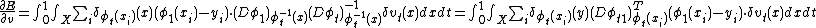- Registering and Matching Information Across Coordiate Systems in CA via Variations
- Dense image matching
- Landmark matching with correspondence
- LDDMM for image and landmark matching: perturbation in the vector fields
- References
{{Draft article|subject=mathematics}}{{Multiple issues|{{lead missing|date=February 2016}}{{technical|date=February 2016}}}}
Registering and Matching Information Across Coordiate Systems in CA via Variations
In CA the geodesics and their coordinates are generated by solving inexact matching problems calculating the geodesic
flows of diffeomorphisms from their start point onto targets. Inexact matching has been examined in many cases and have come to be called Large Deformation Diffeomorphic Metric Mapping (LDDMM) originally solved for landmarks with correspondence [1][2][3][4] and for dense image matching.[5][6] These methods have been extended to landmarks without registration via measure matching,[7] curves,[8] surfaces,[9][10] dense vector[11] and tensor [12] imagery, and varifolds removing orientation.[13] The objects being matched are generally modelled as noisey versions (see below Bayesian statistical modelling section) of the shapes and forms  . The geodesic position and geodesic coordinates associated to Log and Exp are solved as variational problems solving inexact matching of the coordinate systems using classical methods in optimal control.
. The geodesic position and geodesic coordinates associated to Log and Exp are solved as variational problems solving inexact matching of the coordinate systems using classical methods in optimal control.
Matching of coordinates results from introducing an endpoint condition 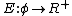 which measures the correspondence or registration of elements in the orbit under coordinate system transformation.
which measures the correspondence or registration of elements in the orbit under coordinate system transformation.
The necessary conditions for a minimizer of 1 satisfies 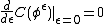 , for perturbation
, for perturbation  , with fixed initial condition,
, with fixed initial condition, 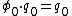 ,
,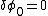 , with free endpoint. This gives the Euler equation interior to
, with free endpoint. This gives the Euler equation interior to  , with a boundary condition at
, with a boundary condition at  where the target enters. Integrating by parts
where the target enters. Integrating by parts 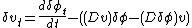 gives
gives
Dense image matching
Dense image matching illustrates one of the two extremes of, the momentum having a vector density pointwise function, so that
for
 a vector function. For dense images the action
a vector function. For dense images the action  implies we will requires the variation of the inverse
implies we will requires the variation of the inverse 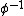 with respect to
with respect to  for the chain rule calculation
for the chain rule calculation 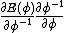 . This requires the identity
. This requires the identity 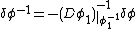 following from the identity
following from the identity 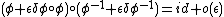 . This is for such function spaces the generalization of the classic matrix perturbation of the inverse.
. This is for such function spaces the generalization of the classic matrix perturbation of the inverse.
The optimizer of Control Problem 1 satisfies the Euler equation with boundary condition at time t=1:
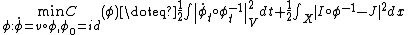
.
Landmark matching with correspondence
Landmark matching demonstrates the singularity of 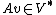 as a generalized function or delta-distribution, since for landmarks,
as a generalized function or delta-distribution, since for landmarks, all of boundary mass is conscentrated on singular subsets of the volume space. The optimizer of Control Problem 1 satisfies the weak Euler equation for delta-distributions:
all of boundary mass is conscentrated on singular subsets of the volume space. The optimizer of Control Problem 1 satisfies the weak Euler equation for delta-distributions:
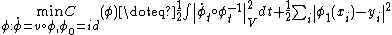
Notice this gives in particular the initial condition.
Taking 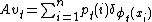 ; conservation
; conservation 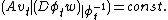 ,
, 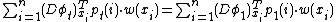
. 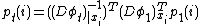 .
.
LDDMM for image and landmark matching: perturbation in the vector fields
The original large deformation diffeomorphic metric mapping (LDDMM) algorithms took variations with respect to the vector field parameterization of the group, since 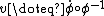 are in a vector spaces. Variations satisfy the necessary optimality conditions..
are in a vector spaces. Variations satisfy the necessary optimality conditions..
- Beg solved the Control Problem for dense image matching maximizing with respect to the velocity field; as did Joshi for Landmark matching.
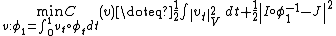
necessary conditions become 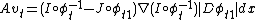 where
where 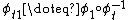 .
.
- Joshi solved the landmark matching problem taking variations with respect ot the vector field:
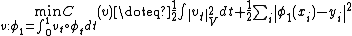 ;
;
necessary conditions become 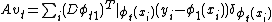 .
.
The perturbation in the vector field requires the identity 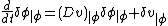 which implies
which implies 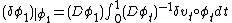 Take the variation in the vector fields
Take the variation in the vector fields 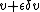 using the chain rule
using the chain rule 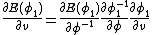 which gives the first variation
which gives the first variation
.
Joshi solved the landmark matching problem optimizing with respect to the velocity field:
References
2. ^{{Cite book|title = Geodesic Interpolating Splines|url = http://dl.acm.org/citation.cfm?id=646596.756898|journal = Proceedings of the Third International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition|date = 2001-01-01|location = London, UK, UK|isbn = 978-3-540-42523-6|pages = 513–527|series = EMMCVPR '01|first = Vincent|last = Camion|first2 = Laurent|last2 = Younes}}
3. ^{{Cite journal|title = Statistics on diffeomorphisms via tangent space representations|pmid = 15501085|journal = NeuroImage|date = 2004-01-01|issn = 1053-8119|pages = S161–169|volume = 23 Suppl 1|doi = 10.1016/j.neuroimage.2004.07.023|first = M.|last = Vaillant|first2 = M. I.|last2 = Miller|first3 = L.|last3 = Younes|first4 = A.|last4 = Trouvé|citeseerx = 10.1.1.132.6802}}
4. ^{{Cite journal|title = A hamiltonian particle method for diffeomorphic image registration|pmid = 17633716|journal = Information Processing in Medical Imaging: Proceedings of the ... Conference|date = 2007-01-01|issn = 1011-2499|pages = 396–407|volume = 20|first = Stephen|last = Marsland|first2 = Robert|last2 = McLachlan}}
5. ^{{Cite journal|title = Computing Large Deformation Metric Mappings via Geodesic Flows of Diffeomorphisms|journal = International Journal of Computer Vision|volume = 61|issue = 2|pages = 139–157|url = https://www.researchgate.net/publication/220660081 |accessdate = 2015-11-22|doi = 10.1023/B:VISI.0000043755.93987.aa|year = 2005|last1 = Beg|first1 = M. Faisal|last2 = Miller|first2 = Michael I|last3 = Trouvé|first3 = Alain|last4 = Younes|first4 = Laurent}}
6. ^{{Cite journal|title = Diffeomorphic 3D Image Registration via Geodesic Shooting Using an Efficient Adjoint Calculation|journal = Int. J. Comput. Vision|date = 2012-04-01|issn = 0920-5691|pages = 229–241|volume = 97|issue = 2|doi = 10.1007/s11263-011-0481-8|first = François-Xavier|last = Vialard|first2 = Laurent|last2 = Risser|first3 = Daniel|last3 = Rueckert|first4 = Colin J.|last4 = Cotter}}
7. ^{{Cite book|title = L.: Diffeomorphic matching of distributions: A new approach for unlabelled point-sets and sub-manifolds matching|volume = 2|pages = 712–718|chapter-url = https://www.researchgate.net/publication/4082354|website = ResearchGate|accessdate = 2015-11-25|doi = 10.1109/CVPR.2004.1315234|chapter = Diffeomorphic matching of distributions: A new approach for unlabelled point-sets and sub-manifolds matching|year = 2004|last1 = Glaunes|first1 = J|last2 = Trouve|first2 = A|last3 = Younes|first3 = L|isbn = 978-0-7695-2158-9|citeseerx = 10.1.1.158.4209}}
8. ^{{Cite journal|title = Large Deformation Diffeomorphic Metric Curve Mapping|pmc = 2858418|journal = International Journal of Computer Vision|date = 2008-12-01|issn = 0920-5691|pmid = 20419045|pages = 317–336|volume = 80|issue = 3|doi = 10.1007/s11263-008-0141-9|first = Joan|last = Glaunès|first2 = Anqi|last2 = Qiu|first3 = Michael I.|last3 = Miller|first4 = Laurent|last4 = Younes}}
9. ^"Vaillant 1149–1159"
10. ^{{Cite journal|title = Surface matching via currents|journal = Proceedings of Information Processing in Medical Imaging (IPMI 2005), Number 3565 in Lecture Notes in Computer Science|date = 2005-01-01|pages = 381–392|first = Marc|last = Vaillant|first2 = Joan|last2 = Glaunès|citeseerx = 10.1.1.88.4666}}
11. ^{{Cite book|title = Large deformation diffeomorphic metric mapping of fiber orientations|url = http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=1544880&url=http%253A%252F%252Fieeexplore.ieee.org%252Fiel5%252F10347%252F32976%252F01544880.pdf%253Farnumber%253D1544880|journal = Tenth IEEE International Conference on Computer Vision, 2005. ICCV 2005|date = 2005-10-01|pages = 1379–1386 Vol. 2|volume = 2|doi = 10.1109/ICCV.2005.132|first = Yan|last = Cao|first2 = M.I.|last2 = Miller|first3 = R.L.|last3 = Winslow|first4 = L.|last4 = Younes|isbn = 978-0-7695-2334-7|citeseerx = 10.1.1.158.1582}}
12. ^{{Cite journal|title = Large deformation diffeomorphic metric mapping of vector fields|url = http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=1501927&url=http%253A%252F%252Fieeexplore.ieee.org%252Fiel5%252F42%252F32229%252F01501927|journal = IEEE Transactions on Medical Imaging|date = 2005-09-01|issn = 0278-0062|pmc = 2848689|pmid = 17427733|pages = 1216–1230|volume = 24|issue = 9|doi = 10.1109/TMI.2005.853923|first = Yan|last = Cao|first2 = M.I.|last2 = Miller|first3 = R.L.|last3 = Winslow|first4 = L.|last4 = Younes|citeseerx = 10.1.1.157.8377}}
13. ^{{Cite journal|title = The Varifold Representation of Nonoriented Shapes for Diffeomorphic Registration|journal = SIAM Journal on Imaging Sciences|date = 2013-01-01|pages = 2547–2580|volume = 6|issue = 4|doi = 10.1137/130918885|first = N.|last = Charon|first2 = A.|last2 = Trouvé|arxiv = 1304.6108 }}
- Juan Carlos Unzue
- Juan Carlos Valenzuela (footballer)
- Juan Carlos Valeron Santana
- Juan Carlos Varela
- Juan Carlos Vellido
- Juan Carlos Virgen
- Juan Carlos Xama
- Juan Carlos Yegros
- Juan Carlos Zaldivar
- Juan Carlos Zaldívar
- Juan Carlos Zaragoza
- Juan Carlos Zarate
- Juan Carlos Zubczuk
- Juan Carlos Zuniga
- Juan Carone
- Juan Carrasco (explorer)
- Juan Carrasco (general)
- Juan Carreno
- Juan Carreño López
- Juan Carreño Miranda
- Juan Carulla
- Juan Casco
- Juan Casiano
- Juan Castaneda
- Juan Castano