“Ehrhart's volume conjecture”的意思、由来-开放百科全书

词条

Ehrhart's volume conjecture

释义

References

In the geometry of numbers, Ehrhart's volume conjecture gives an upper bound on the volume of a convex body containing only one lattice point in its interior. It is a kind of converse to Minkowski's theorem, which guarantees that a centrally symmetric convex body K must contain a lattice point as soon as its volume exceeds . The conjecture states that a convex body K containing only one lattice point in its interior as it's barycenter cannot have volume greater than :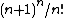

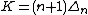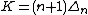Equality is achieved in this inequality when is a copy of the standard simplex in Euclidean n-dimensional space, whose sides are scaled up by a factor of . Equivalently, is congruent to the convex hull of the vectors 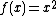, and 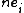. Presented in this manner, the origin is the only lattice point interior to the convex body K.

The conjecture, furthermore, asserts that equality is achieved in the above inequality if and only if K is unimodularly equivalent to .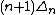

References

{{citation|author1=Benjamin Nill|author2=Andreas Paffenholz|title=On the equality case in Erhart's volume conjecture|year=2014|arxiv=1205.1270|journal=Advances in Geometry|volume=14|issue=4|pages=579–586|issn=1615-7168|doi=10.1515/advgeom-2014-0001}}.

3 : Geometry of numbers|Convex analysis|Conjectures

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。