“Engelbert–Schmidt zero–one law”的意思、由来-开放百科全书

词条

Engelbert–Schmidt zero–one law

释义

Engelbert–Schmidt 0–1 law
See also
References

The Engelbert–Schmidt zero–one law is a theorem that gives a mathematical criterion for an event associated with a continuous, non-decreasing additive functional of Brownian motion to have probability either 0 or 1, without the possibility of an intermediate value. This zero-one law is used in the study of questions of finiteness and asymptotic behavior for stochastic differential equations.^[1] (A Wiener process is a mathematical formalization of Brownian motion used in the statement of the theorem.) This 0-1 law, published in 1981, is named after Hans-Jürgen Engelbert^[2] and the probabilist Wolfgang Schmidt^[3] (not to be confused with the number theorist Wolfgang M. Schmidt).

Engelbert–Schmidt 0–1 law

Let be a σ-algebra and let 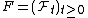be an increasing family of sub-σ-algebras of . Let 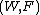be a Wiener process on the probability space .

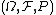Suppose that is a Borel measurable function of the real line into [0,∞].

Then the following three assertions are equivalent:

(i)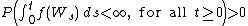

(ii)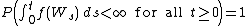

(iii)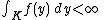

for all compact subsets of the real line.^[4]

References

1. ^{{cite book|author=Karatzas, Ioannis|author2=Shreve, Steven|title=Brownian motion and stochastic calculus|publisher=Springer|year=2012|pages=215|url=https://books.google.com/books?id=ATNy_Zg3PSsC&pg=PA215}}
2. ^{{MathGenealogy|id=29366|title=Hans-Jürgen Engelbert}}
3. ^{{MathGenealogy|id=90300|title=Wolfgang Schmidt}}
4. ^{{cite book|author=Engelbert, H. J.|author2=Schmidt, W.|chapter=On the behavior of certain functionals of the Wiener process and applications to stochastic differential equations|editor=Arató, M.|editor2=Vermes, D.|editor3=Balakrishnan, A. V.|title=Stochastic Differential Systems|series=Lectures Notes in Control and Information Sciences, vol. 36|year=1981|publisher=Springer|location=Berlin; Heidelberg|pages=47–55|doi=10.1007/BFb0006406}}

1 : Probability theorems

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Engelbert–Schmidt 0–1 law

See also

References