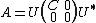- Properties
- Decomposition
- References
In mathematics, an EP matrix (or range-Hermitian matrix[1] or RPN matrix[2]) is a matrix A whose range is equal to the range of its conjugate transpose A*. Another equivalent characterization of EP matrices is that the range of A is orthogonal to the nullspace of A. Thus, EP matrices are also known as RPN matrices, with RPN meaning Range Perpendicular to Nullspace.
EP matrices were introduced in 1950 by Hans Schwerdtfeger,[1][3] and since then, many equivalent characterizations of EP matrices have been investigated through the literature.[4] The meaning of the EP abbreviation stands originally for Equal Principal, but it is widely believed that it stands for Equal Projectors instead, since an equivalent characterization of EP matrices is based in terms of equality of the projectors AA+ and A+A.[5]
According to the fundamental theorem of linear algebra, the range of any matrix A is equal to the null-space of A*, but is not necessarily equal to the null-space of A. When A is an EP matrix, the range of A is precisely equal to the null-space of A.
Properties
- An equivalent characterization of an EP matrix A is that A commutes with its Moore-Penrose inverse, that is, the projectors AA+ and A+A are equal. This is similar to the characterization of normal matrices where A commutes with its conjugate transpose.[4] As a corollary, nonsingular matrices are always EP matrices.
- The sum of EP matrices Ai is an EP matrix if the null-space of the sum is contained in the null-space of each matrix Ai.[6]
- To be an EP matrix is a necessary condition for normality: A is normal if and only if A is EP matrix and AAA2 = A2AA.[4]
- When A is an EP matrix, the Moore-Penrose pseudoinverse of A is equal to the group inverse of A.[4]
- A is an EP matrix if and only if the Moore-Penrose pseudoinverse of A is an EP matrix.[4]
Decomposition
The spectral theorem states that a matrix is normal if and only if it is unitarily similar to a diagonal matrix.
Weakening the normality condition to EPness, an alike statement is still valid. Precisely, a matrix is an EP matrix if and only if it is unitarily similar to a core-nilpotent matrix[2], that is,
where U is an orthogonal matrix and C is a nonsingular matrix.
References
2. ^1 {{Cite book|url=https://www.worldcat.org/oclc/43662189|title=Matrix analysis and applied linear algebra|last=Meyer|first=Carl D.|date=2000|publisher=Society for Industrial and Applied Mathematics|year=|isbn=0898714540|location=Philadelphia|pages=|oclc=43662189}}
3. ^{{Cite book|title=Introduction to linear algebra and the theory of matrices|last=Schwerdtfeger|first=Hans|publisher=P. Noordhoff|year=1950|isbn=|location=|pages=}}
4. ^1 2 3 4 {{Cite journal|last=Cheng|first=Shizhen|last2=Tian|first2=Yongge|date=2003-12-01|title=Two sets of new characterizations for normal and EP matrices|url=http://www.sciencedirect.com/science/article/pii/S0024379503006505|journal=Linear Algebra and its Applications|volume=375|pages=181–195|doi=10.1016/S0024-3795(03)00650-5|issn=0024-3795|via=}}
5. ^{{Cite book|url=https://www.worldcat.org/oclc/1023540775|title=Scalar, Vector, and Matrix Mathematics : Theory, Facts, and Formulas.|last=S.|first=Bernstein, Dennis|date=2018|publisher=Princeton University Press|isbn=9781400888252|location=Princeton|oclc=1023540775}}
6. ^{{Cite journal|last=Meenakshi|first=A.R.|date=1983|title=On sums of EP matrices|url=http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.638.7389|journal=Houston Journal of Mathematics|volume=9|pages=|via=}}
- Neda Naldi
- Neda plutella
- Nedarim (Talmud)
- Ned Azemia
- Ned Baptiste
- Ned Barnie
- Ned Bell
- Ned Buntline bibliography
- Ned Burton
- Ned Carew
- Ned Carey
- Ned C. Cole
- Ned C. Cole Jr
- Ned C. Cole, Jr
- Ned C. Cole, jr
- Ned C. Cole Jr.
- Ned C. Cole, jr.
- Ned C. Cole jr.
- Ned C. Cole jr
- Ned C. Cole, Jr.
- Ned C. Cole Junior
- Ned C. Cole, junior
- Ned C. Cole junior
- Ned C. Cole, Junior
- Ned Chawke