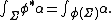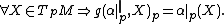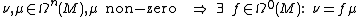- Notation Manifold k-forms Omitted elements of a sequence Exterior product Lie bracket Exterior derivative Tangent maps Pull-back Musical isomorphisms Interior product Hodge star Co-differential operator Oriented manifold Volume form Area form Inner product for k-forms Lie derivative Levi-Civita connection Covariant derivative Laplace–Beltrami operator
- Important Definitions Definitions on Ωk(M) Cohomology Dirichlet energy Definitions on metric g Lagrangian derivative
- Properties Exterior derivative properties Exterior product properties Pull-back properties Musical isomorphism properties Inner product properties Hodge star properties Co-differential operator properties Lie derivative properties Levi-Civita connection properties Covariant derivative
- Exterior calculus identities Dimensions Exterior products Projection and rejection Sum expressions Hodge decomposition Poincaré lemma
- Relations to vector calculus Identities in Euclidean 3-space Lie derivatives Laplacian
- References
This article summarizes important identities in exterior calculus.[1][2][3][4][5]
Notation
The following summarizes short definitions and notations that are used in this article.
Manifold
 ,
,  are
are  -dimensional smooth manifolds, where
-dimensional smooth manifolds, where  . That is, differentiable manifolds that can be differentiated enough times for the purposes on this page.
. That is, differentiable manifolds that can be differentiated enough times for the purposes on this page.
 ,
,  denote two points on the manifolds.
denote two points on the manifolds.
 is the tangent bundle of the smooth manifold
is the tangent bundle of the smooth manifold  .
.
 ,
,  denote the tangent spaces of
denote the tangent spaces of  ,
,  at the points
at the points  ,
,  , respectively.
, respectively.
Sections of the tangent bundles, also known as vector fields, are typically denoted as 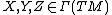 such that at a point
such that at a point  we have
we have  .
.
Given an inner product 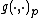 on each
on each  , the manifold becomes a Riemannian manifold.
, the manifold becomes a Riemannian manifold.
The boundary of a manifold  is a manifold
is a manifold  , which has dimension
, which has dimension  . An orientation on
. An orientation on  induces an orientation on
induces an orientation on  .
.
We usually denote a submanifold by  .
.
k-forms
 -forms are differential forms defined on
-forms are differential forms defined on  . We denote the set of all
. We denote the set of all  -forms as
-forms as  . For
. For  we usually write
we usually write  ,
,  ,
,  .
.
 -forms
-forms  are just scalar functions
are just scalar functions 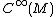 on
on  .
.  denotes the constant
denotes the constant  -form equal to
-form equal to  everywhere.
everywhere.
Omitted elements of a sequence
When we are given 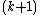 inputs
inputs  and a
and a  -form
-form  we omit the
we omit the  th entry by writing
th entry by writing
Exterior product
The exterior product is also known as the wedge product. It is denoted by 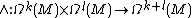 . The exterior product of a
. The exterior product of a  -form
-form  and an
and an  -form
-form  produce a
produce a  -form
-form  . It can be written using the set
. It can be written using the set  of all permutations
of all permutations  of
of  such that
such that  as
as
Lie bracket
The Lie bracket of sections  is defined as the unique section
is defined as the unique section  that satisfies
that satisfies
Exterior derivative
The exterior derivative  is defined for all
is defined for all  . We generally omit the subscript when it is clear from the context.
. We generally omit the subscript when it is clear from the context.
For a  -form
-form  we have
we have  as the directional derivative
as the directional derivative  -form. i.e. in the direction
-form. i.e. in the direction  we have
we have 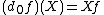 .{{citation needed|reason=The notation Xf is only defined in words, and its use here is confusing.|date=November 2018}}
.{{citation needed|reason=The notation Xf is only defined in words, and its use here is confusing.|date=November 2018}}
For  ,
,
Tangent maps
If  is a smooth map, then
is a smooth map, then 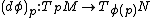 defines a tangent map from
defines a tangent map from  to
to  . It is defined through curves
. It is defined through curves  on
on  with derivative
with derivative 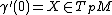 such that
such that
Note that  is a
is a  -form with values in
-form with values in  .
.
Pull-back
If  is a smooth map, then the pull-back of a
is a smooth map, then the pull-back of a  -form
-form  is defined such that for any
is defined such that for any  dimensional submanifold
dimensional submanifold 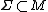
The pull-back can also be expressed as
Musical isomorphisms
Given a section  there exists a
there exists a  -form
-form  such that on each
such that on each 
We call this mapping the flat operator  .
.
Given a  -form
-form  there exists a section
there exists a section  such that on each
such that on each 
We call this mapping the sharp operator  .
.  and
and  constitute the musical isomorphisms.
constitute the musical isomorphisms.
Interior product
Also known as the interior derivative, the interior product given a section  is a map
is a map  that effectively substitutes the first input of a
that effectively substitutes the first input of a 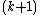 -form with
-form with  . If
. If 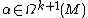 and
and  then
then
Hodge star
The Hodge star operator  is defined as such that it maps
is defined as such that it maps  -forms
-forms  to their dual
to their dual  -form
-form 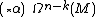 .
.
For example, if  is a positively oriented frame for
is a positively oriented frame for  according to the given metric
according to the given metric  , then
, then
We omit to write the dimension  or inversion symbol
or inversion symbol  with the Hodge star operator as it is evident in the context.
with the Hodge star operator as it is evident in the context.
We call  the signature of the metric
the signature of the metric  . For example in Minkowski space
. For example in Minkowski space  and in Riemannian manifolds
and in Riemannian manifolds  .
.
Co-differential operator
The co-differential operator 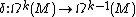 on an
on an  dimensional manifold
dimensional manifold  is defined by
is defined by
Oriented manifold
An  -dimensional orientable manifold
-dimensional orientable manifold  is a manifold that can be equipped with a choice of a non-zero
is a manifold that can be equipped with a choice of a non-zero  -form
-form  .
.
Volume form
On a orientable manifold  the canonical choice of a volume form given a metric
the canonical choice of a volume form given a metric  is
is 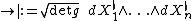 for any positively oriented basis
for any positively oriented basis  .
.
Area form
Given a volume form  and a unit normal vector
and a unit normal vector  we can also define an area form
we can also define an area form  on the {{nowrap|boundary
on the {{nowrap|boundary  }}
}}
Inner product for k-forms
The inner product between two  -forms
-forms  is defined pointwise on
is defined pointwise on  by
by
The  -inner product for the space of
-inner product for the space of  -forms
-forms  is defined by
is defined by
Lie derivative
We define the Lie derivative  through Cartan's magic formula for a given section
through Cartan's magic formula for a given section  as
as
It describes the change of a  -form along a flow map
-form along a flow map  associated to the section
associated to the section  .
.
Laplace–Beltrami operator
The Laplacian  is defined as
is defined as  .
.
Important Definitions
Definitions on Ωk(M)
 is called...
is called...
- closed if

- exact if

- coclosed if

- coexact if

- harmonic if closed and coclosed
Cohomology
The  -th cohomology of a manifold
-th cohomology of a manifold  and its exterior derivative operators
and its exterior derivative operators  is given by
is given by
Two closed  -forms
-forms  are in the same cohomology class if their difference is an exact form i.e.
are in the same cohomology class if their difference is an exact form i.e.
A closed surface of genus  will have
will have  generators which are harmonic.
generators which are harmonic.
Dirichlet energy
Given 
Properties
Exterior derivative properties
( Stokes' theorem )
( Nilpotent )
if
( Leibniz rule )
if
( Directional derivative )
if
Exterior product properties
if
( Anticommutative )
( Associativity )
for
( Distributivity of scalar multiplication )
( Distributivity over addition )
when
. The rank of a
-form
is defined as the minimum number of terms, each consisting of the exterior product of

-forms, that can be summed to produce
.
Pull-back properties
( Commutative with
)
( Distributes over
)
( Contravariant )
for
( Function composition )
Musical isomorphism properties
Inner product properties
( Nilpotent )
for
( Leibniz rule )
for
for
for
Hodge star properties
for
( Linearity )
( Inversion )
for
( Commutative with
-forms )
for
( Hodge star preserves
-form norm )
( The Hodge dual of the constant function 1 is the volume form )
Co-differential operator properties
( Nilpotent )
( Hodge adjoint to
)
if
(
adjoint to
)
if
Lie derivative properties
( Commutative with
)
( Commutative with
)
( Leibniz rule )
Exterior calculus identities
if
if
( Inner product )
(Jacobi identity)
Dimensions
If 
for
for
If  is a basis, then a basis of
is a basis, then a basis of  is
is
Exterior products
Projection and rejection
( Interior product
dual to wedge
)
for
If  , then
, then
 is the projection of
is the projection of  onto the orthogonal complement of
onto the orthogonal complement of  .
.
 is the rejection of
is the rejection of  , the remainder of the projection.
, the remainder of the projection.
- thus
 ( Projection rejection decomposition )
( Projection rejection decomposition )
Given the boundary  with unit normal vector
with unit normal vector 
 extracts the tangential component of the boundary.
extracts the tangential component of the boundary.
 extracts the normal component of the boundary.
extracts the normal component of the boundary.
Sum expressions
given a positively oriented orthonormal frame
.
Hodge decomposition
If  ,
,  such that
such that
Poincaré lemma
If  has only one cohomology class
has only one cohomology class  and no boundary
and no boundary  , then for any closed
, then for any closed  such that
such that
Relations to vector calculus
{{See also|Vector calculus identities}}Identities in Euclidean 3-space
Let Euclidean metric  .
.
We use  differential operator
differential operator 
for
.
( Cross product )
-
 if
if 
( Dot product )
( Gradient
-form )
( Directional derivative )
( Divergence )
( Curl )
where
is the unit normal vector of
and
is the area form on
.
( Divergence theorem )
Lie derivatives
(
-forms )
(
-forms )
if
(
-forms on
-manifolds )
if
(
-forms )
References
2. ^{{cite book |last1=Schwarz |first1=Günter |title=Hodge Decomposition – A Method for Solving Boundary Value Problems |date=1995 |publisher=Springer |isbn=978-3-540-49403-4}}
3. ^{{cite book |last1=Cartan |first1=Henri |title=Differential forms |publisher=Dover Publications |isbn=978-0486450100 |edition=Dover}}
4. ^{{cite book |last1=Bott |first1=Raoul |last2=Tu |first2=Loring W. |title=Differential forms in algebraic topology |publisher=Springer |isbn=978-0387906133}}
5. ^{{cite book |last1=Abraham |first1=Ralph |last2=J.E. |first2=Marsden |last3=Ratiu |first3=Tudor |title=Manifolds, tensor analysis, and applications |publisher=Springer-Verlag |isbn=978-1-4612-1029-0 |edition=2nd}}
- Alex Borgia
- Alex Borteh
- Alex Bourret
- Alex Box Stadium
- Alex Boyd (photographer)
- Alex Bradley (basketball)
- Alex brandon
- Alex Brandon
- Alex Brimeyer
- Alex brimyear
- Alex Brink
- Alex Brink (geneticist)
- Alex Brooks
- Alex Brosque
- Alex Broun
- Alex Brown (American football)
- Alex. Brown & Co
- Alex Browne (filmmaker)
- Alex Brown (football player)
- Alex. Brown & Sons
- Alex Bruce (footballer, born 1984)
- Alex Bruford
- Alex Brummer
- Alex Bruno
- Alex Buchman