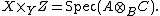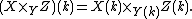1. Definition

2. Interpretations and special cases

3. Base change and descent

4. Notes

5. References

6. External links

In mathematics, specifically in algebraic geometry, the fiber product of schemes is a fundamental construction. It has many interpretations and special cases. For example, the fiber product describes how an algebraic variety over one field determines a variety over a bigger field, or the pullback of a family of varieties, or a fiber of a family of varieties. Base change is a closely related notion.

Definition

The category of schemes is a broad setting for algebraic geometry. A fruitful philosophy (known as Grothendieck's relative point of view) is that much of algebraic geometry should be developed for a morphism of schemes X → Y (called a scheme X over Y), rather than for a single scheme X. For example, rather than simply studying algebraic curves, one can study families of curves over any base scheme Y. Indeed, the two approaches enrich each other.

In particular, a scheme over a commutative ring R means a scheme X together with a morphism X → Spec(R). The older notion of an algebraic variety over a field k is equivalent to a scheme over k with certain properties. (There are different conventions for exactly which schemes should be called "varieties". One standard choice is that a variety over a field k means an integral separated scheme of finite type over k.^[1])

In general, a morphism of schemes X → Y can be imagined as a family of schemes parametrized by the points of Y. Given a morphism from some other scheme Z to Y, there should be a "pullback" family of schemes over Z. This is exactly the fiber product X x_Y Z → Z.

Formally: it is a useful property of the category of schemes that the fiber product always exists.^[2] That is, for any morphisms of schemes X → Y and Z → Y, there is a scheme X ×_Y Z with morphisms to X and Z, making the diagram

commutative, and which is universal with that property. That is, for any scheme W with morphisms to X and Z whose compositions to Y are equal, there is a unique morphism from W to X ×_Y Z that makes the diagram commute. As always with universal properties, this condition determines the scheme X ×_Y Z up to a unique isomorphism, if it exists. The proof that fiber products of schemes always do exist reduces the problem to the tensor product of commutative rings. In particular, when X, Y, and Z are all affine schemes, so X = Spec(A), Y = Spec(B), and Z = Spec(C) for some commutative rings A,B,C, the fiber product is the affine scheme

The morphism X x_Y Z → Z is called the base change or pullback of the morphism X → Y via the morphism Z → Y.

Interpretations and special cases

• In the category of schemes over a field k, the product X × Y means the fiber product X ×_k Y (which is shorthand for the fiber product over Spec(k)). For example, the product of affine spaces A^m and Aⁿ over a field k is the affine space A^m+n over k.
• For a scheme X over a field k and any field extension E of k, the base change X_E means the fiber product X ×_Spec(k) Spec(E). Here X_E is a scheme over E. For example, if X is the curve in the projective plane P{{supsub|2|R}} over the real numbers R defined by the equation xy² = 7z³, then X_C is the complex curve in P{{supsub|2|C}} defined by the same equation. Many properties of an algebraic variety over a field k can be defined in terms of its base change to the algebraic closure of k, which makes the situation simpler.
• Let f: X → Y be a morphism of schemes, and let y be a point in Y. Then there is a morphism Spec(k(y)) → Y with image y, where k(y) is the residue field of y. The fiber of f over y is defined as the fiber product X ×_Y Spec(k(y)); this is a scheme over the field k(y).^[3] This concept helps to justify the rough idea of a morphism of schemes X → Y as a family of schemes parametrized by Y.
• Let X, Y, and Z be schemes over a field k, with morphisms X → Y and Z → Y over k. Then the set of k-rational points of the fiber product X x_Y Z is easy to describe:

That is, a k-point of X x_Y Z can be identified with a pair of k-points of X and Z that have the same image in Y. This is immediate from the universal property of the fiber product of schemes.

• If X and Z are closed subschemes of a scheme Y, then the fiber product X x_Y Z is exactly the intersection X ∩ Z, with its natural scheme structure.^[4] The same goes for open subschemes.

Base change and descent

Some important properties P of morphisms of schemes are preserved under arbitrary base change. That is, if X → Y has property P and Z → Y is any morphism of schemes, then the base change X x_Y Z → Z has property P. For example, flat morphisms, smooth morphisms, proper morphisms, and many other classes of morphisms are preserved under arbitrary base change.^[5]

The word descent refers to the reverse question: if the pulled-back morphism X x_Y Z → Z has some property P, must the original morphism X → Y have property P? Clearly this is impossible in general: for example, Z might be the empty scheme, in which case the pulled-back morphism loses all information about the original morphism. But if the morphism Z → Y is flat and surjective (also called faithfully flat) and quasi-compact, then many properties do descend from Z to Y. Properties that descend include flatness, smoothness, properness, and many other classes of morphisms.^[6] These results form part of Grothendieck's theory of faithfully flat descent.

Example: for any field extension k ⊂ E, the morphism Spec(E) → Spec(k) is faithfully flat and quasi-compact. So the descent results mentioned imply that a scheme X over k is smooth over k if and only if the base change X_E is smooth over E. The same goes for properness and many other properties.

Notes

References

• {{EGA|book=I}}
• {{Hartshorne AG}}

External links

• {{Citation | author1=The Stacks Project Authors | title=The Stacks Project | url=http://stacks.math.columbia.edu/}}

• Anaerobicly digested
• Anaerobic methane oxidation
• Anaerobic microorganism
• Anaerobic oxidation of methane
• Anaerobic pathways
• Anaerobic Process
• Anaerobic process
• Anaerobics
• Anaeroplasmatales
• Anaesthesiologist
• Anaesthetic agent
• Anaesthetic agents
• Anaesthetic drugs
• Anaesthetic technician
• Anaesthetize
• Ana faris
• An Affair
• An Affair of Honor
• An affair of honor
• An affair to forget
• An Affair to Forget
• An Affair to Forget (disambiguation)
• An Affair To Forget (Will & Grace)
• An affair to remember
• An Affirming Flame (Andromeda)