- Definition
- Properties
- Extensions to singular operators Algebraic extension Analytic extension
- Generalizations
- References
In mathematics, the Fuglede−Kadison determinant of an invertible operator in a finite factor is a positive real number associated with it. It defines a multiplicative homomorphism from the set of invertible operators to the set of positive real numbers. The Fuglede−Kadison determinant of an operator  is often denoted by
is often denoted by  .
.
For a matrix  in
in  ,
,  which is the normalized form of the absolute value of the determinant of
which is the normalized form of the absolute value of the determinant of  .
.
Definition
Let  be a finite factor with the canonical normalized trace
be a finite factor with the canonical normalized trace  and let
and let  be an invertible operator in
be an invertible operator in  . Then the Fuglede−Kadison determinant of
. Then the Fuglede−Kadison determinant of  is defined as
is defined as
(cf. Relation between determinant and trace via eigenvalues). The number 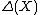 is well-defined by continuous functional calculus.
is well-defined by continuous functional calculus.
Properties
-
 for invertible operators
for invertible operators 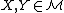 ,
, -
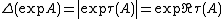 for
for 
-
 is norm-continuous on
is norm-continuous on  , the set of invertible operators in
, the set of invertible operators in 
-
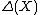 does not exceed the spectral radius of
does not exceed the spectral radius of  .
.
Extensions to singular operators
There are many possible extensions of the Fuglede−Kadison determinant to singular operators in  . All of them must assign a value of 0 to operators with non-trivial nullspace. No extension of the determinant
. All of them must assign a value of 0 to operators with non-trivial nullspace. No extension of the determinant  from the invertible operators to all operators in
from the invertible operators to all operators in  , is continuous in the uniform topology.
, is continuous in the uniform topology.
Algebraic extension
The algebraic extension of  assigns a value of 0 to a singular operator in
assigns a value of 0 to a singular operator in  .
.
Analytic extension
For an operator  in
in  , the analytic extension of
, the analytic extension of  uses the spectral decomposition of
uses the spectral decomposition of  to define
to define  with the understanding that
with the understanding that  if
if  . This extension satisfies the continuity property
. This extension satisfies the continuity property
for
Generalizations
Although originally the Fuglede−Kadison determinant was defined for operators in finite factors, it carries over to the case of operators in von Neumann algebras with a tracial state ( ) in the case of which it is denoted by
) in the case of which it is denoted by 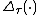 .
.
References
- {{citation
| last1 = Fuglede | first1 = Bent
| last2 = Kadison | first2 = Richard
| journal = Ann. Math. |series=Series 2
| pages = 520−530
| title = Determinant theory in finite factors
| volume = 55
| year = 1952}}.
- {{citation
| last = de la Harpe| first = Pierre
| journal = Proc. Natl. Acad. Sci. USA
| pages = 15864–15877
| title = Fuglede−Kadison determinant: theme and variations
| volume = 110
| year = 2013}}.{{DEFAULTSORT:Fuglede-Kadison determinant}}
- Heinrich XIV, Prince Reuss of Schleiz
- Heinrich XIV, Prince Reuss Younger Line
- Heinrich XIX, Prince Reuss of Greiz
- Heinrich XLV, Hereditary Prince Reuss of Schleiz
- Heinrich XLV, Hereditary Prince Reuss Younger Line
- Heinrich XLV, Prince Reuss
- Heinrich XV, Prince of Reuss-Plauen
- Heinrich XXII
- Heinrich XXII, Prince Reuss-Greiz
- Heinrich XXII, Prince Reuss of Greiz
- Heinrich XXIV, Count of Reuss-Ebersdorf
- Heinrich XXIV, Prince of Reuss-Kostritz
- Heinrich XXIV, Prince of Reuss-Köstritz
- Heinrich XXIV, Prince Reuss of Greiz
- Heinrich XXIV, Prinz Reuss
- Heinrich XXIV Reuss of Köstritz
- Heinrich XX, Prince Reuss of Greiz
- Heinrich XXVII, Prince Reuss of Schleiz
- Heinrich XXVII, Prince Reuss Younger Line
- Heinrich Ysaac
- Heinrich Ysaak
- Heinrich Ziegler
- Heinrich Zimmer (Celticist)
- Heinrich Zoellner
- Heinrich Zoelly

