“Governing equation”的意思、由来-开放百科全书

The governing equations of a mathematical model describe how the values of the unknown variables (i.e. the dependent variables) change when one or more of the known (i.e. independent) variables change.

Mass balance

A mass balance, also called a material balance, is an application of conservation of mass to the analysis of physical systems. It is the simplest governing equation, and it is simply a budget (balance calculation) over the quantity in question:

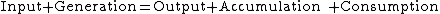
Differential equation

Physics

Classical continuum mechanics

The basic equations in classical continuum mechanics are all balance equations, and as such each of them contains a time-derivative term which calculates how much the dependent variable change with time. For an isolated, frictionless / inviscid system the first four equations are the familiar conservation equations in classical mechanics.

Darcy's law of groundwater flow has the form of a volumetric flux caused by a pressure gradient. A flux in classical mechanics is normally not a governing equation, but usually a defining equation for transport properties. Darcy's law was originally established as an empirical equation, but is later shown to be derivable as an approximation of Navier-Stokes equation combined with an empirical composite friction force term. This explains the duality in Darcy's law as a governing equation and a defining equation for absolute permeability.

The non-linearity of the material derivative in balance equations in general, and the complexities of Cauchy's momentum equation and Navier-Stokes equation makes the basic equations in classical mechanics exposed to establishing of simpler approximations.

Some examples of governing differential equations in classical continuum mechanics are

Biology

Sequence of states

A governing equation may also be a state equation, an equation describing the state of the system, and thus actually be a constitutive equation that has "stepped up the ranks" because the model in question was not meant to include a time-dependent term in the equation. This is the case for a model of an oil production plant which on the average operates in a steady state mode. Results from one thermodynamic equilibrium calculation are input data to the next equilibrium calculation together with some new state parameters, and so on. In this case the algorithm and sequence of input data form a chain of actions, or calculations, that describes change of states from the first state (based solely on input data) to the last state that finally comes out of the calculation sequence.

See also

References

1. ^{{cite book|last1=Fletcher|first1=Clive A.J.|year=1991|title=Computational Techniques for Fluid Dynamics 2; Chapter 1; Fluid Dynamics: The Governing Equations |pages= 1-46|volume=2|publisher=Springer Berlin Heidelberg|location=Berlin / Heidelberg, Germany|isbn=978-3-642-58239-4}}
2. ^{{cite book|last1=Kline|first1=S.J.|year=2012|title=Similitude and Approximation Theory|edition=2012|publisher=Springer Science & Business Media|location=Berlin / Heidelberg, Germany|isbn=9783642616389}}
3. ^{{cite book|last1=Nakariakov|first1=Prof. Valery|year=2015|title=Lecture PX392 Plasma Electrodynamics |edition= Lecture PX392 2015-2016|publisher=Department of Physics, University of Warwick|location= Coventry, England, UK}}[https://www2.warwick.ac.uk/fac/sci/physics/research/cfsa/people/valery/teaching/px420/addres/mhd_int1.pdf]
4. ^{{cite book|last1=Tryggvason|first1=Viola D. Hank Professor Gretar|year=2011|title=Lecture 28 Computational Fluid Dynamics - CFD Course from B. Daly (1969) Numerical methods|edition= Lecture 28 CFD Course 2011|publisher=Department of Aerospace and Mechanical Engineering, University of Notre Dame|location= Notre Dame, Indiana, US}}
5. ^{{cite book|last1=Münchow |first1=Physical Oceanographer Ph.D. Andreas|year=2012|title=Lecture MAST-806 Geophysical Fluid Dynamics |edition=Lecture MAST-806 2012|publisher=University of Delaware|location=Newark, Delaware, US}}
6. ^{{cite book|last1=Brenner|first1=Glover Prof. Michael P.|year=2000|title=The dynamics of thin sheets of fluid Part 1 Water bells by G.I. Taylor|edition=MIT course number 18.325 Spring 2000 |publisher=Harvard University|location=Cambridge, Massachusetts, US}}