“Grassmann graph”的意思、由来-开放百科全书

词条

Grassmann graph

释义

Graph-theoretic properties
Automorphism group
Intersection array
Spectrum
References

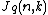{{Infobox graph|name=Grassmann Graph|namesake=Hermann Grassmann|notation=

|vertices=

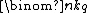|edges=

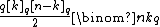|properties=Distance-transitive
Connected|diameter=

}}

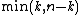Grassmann graphs are a special class of simple graphs defined from systems of subspaces. The vertices of the Grassmann graph 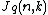are the 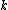-dimensional subspaces of an -dimensional vector space over a finite field of order ; two vertices are adjacent when their intersection is 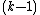-dimensional.

Many of the parameters of Grassmann graphs are -analogs of the parameters of Johnson graphs, and Grassmann graphs have several of the same graph properties as Johnson graphs.

Graph-theoretic properties

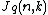is isomorphic to .
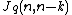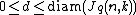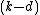For all , the intersection of any pair of vertices at distance is -dimensional.
which is to say that the clique number of 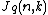is given by an expression in terms its least and greatest eigenvalues 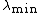and .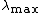

Automorphism group

There is a distance-transitive subgroup of 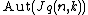isomorphic to the projective linear group .

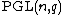In fact, unless 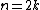or 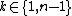, 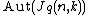{{math|≅}} 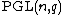; otherwise 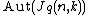{{math|≅}} 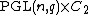or 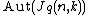{{math|≅}} 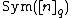respectively.^[1]

Intersection array

As a consequence of being distance-transitive, 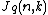is also distance-regular. Letting denote its diameter, the intersection array of 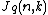is given by 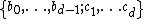where:

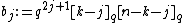for all .
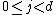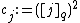for all .

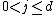Spectrum

The characteristic polynomial of 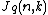is given by

.^[1]

References

1. ^¹{{Cite book|url=https://www.worldcat.org/oclc/851840609|title=Distance-Regular Graphs|last=Brouwer|first=Andries E.|date=1989|publisher=Springer Berlin Heidelberg|others=Cohen, Arjeh M., Neumaier, Arnold.|isbn=9783642743436|location=Berlin, Heidelberg|oclc=851840609}}

2 : Parametric families of graphs|Regular graphs

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。