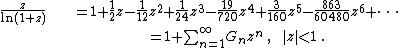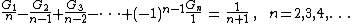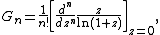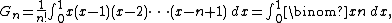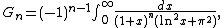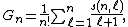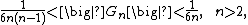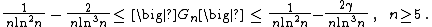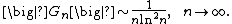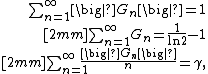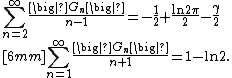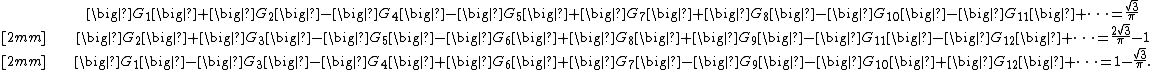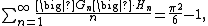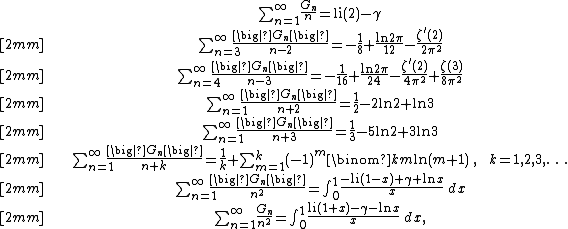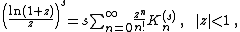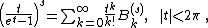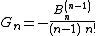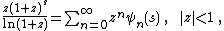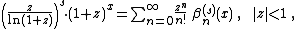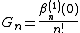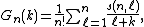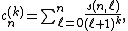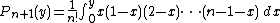请输入您要查询的百科知识：

　

词条 Gregory coefficients
释义

  1. Computation and representations

  2. Bounds and asymptotic behavior

  3. Series with Gregory coefficients

  4. Generalizations

  5. See also

  6. References

Gregory coefficients {{math|Gn}}, also known as reciprocal logarithmic numbers, Bernoulli numbers of the second kind, or Cauchy numbers of the first kind,[1][2][3][3][4][6][5][6][7][10][11][8][9][10] are the rational numbers

n{{math|1{{math|2{{math|3{{math|4{{math|5{{math|6{{math|7{{math|8{{math|9{{math|10{{math|11{{math|...OEIS sequences
Gn+{{sfrac|1|2}}}}−{{sfrac|1|12}}}}+{{sfrac|1|24}}}}−{{sfrac|19|720}}}}+{{sfrac|3|160}}}}−{{sfrac|863|60480}}}}+{{sfrac|275|24192}}}}−{{sfrac|33953|3628800}}}}+{{sfrac|8183|1036800}}}}−{{sfrac|3250433|479001600}}}}+{{sfrac|4671|788480}}}}...}}id=A002206}} (numerators),{{OEIS2C|id=A002207}} (denominators)

that occur in the Maclaurin series expansion of the reciprocal logarithm

Gregory coefficients are alternating {{math|Gn {{=}} (−1)n−1{{!}}Gn{{!}}}} and decreasing in absolute value. These numbers are named after James Gregory who introduced them in 1670 in the numerical integration context. They were subsequently rediscovered by many famous mathematicians and often appear in works of modern authors who do not recognize them.[1][4][17][11][19][20]

Computation and representations

The simplest way to compute Gregory coefficients is to use the recurrence formula

with {{math|G1 {{=}} {{sfrac|1|2}}}}.[12][22] Gregory coefficients may be also computed explicitly via the following differential

the integral

Schröder's integral formula[13][14]

or the finite summation formula

where {{math|s(n,ℓ)}} are the signed Stirling numbers of the first kind.

Bounds and asymptotic behavior

The Gregory coefficients satisfy the bounds

given by Johan Steffensen.[11] These bounds were later improved by various authors. The best known bounds for them were given by Blagouchine.[15] In particular,

Asymptotically, at large index {{math|n}}, these numbers behave as[2][15][13]

More accurate description of {{math|Gn}} at large {{math|n}} may be found in works of Van Veen,[16] Davis,[17] Coffey,[18] Nemes[19] and Blagouchine.[15]

Series with Gregory coefficients

Series involving Gregory coefficients may be often calculated in a closed-form. Basic series with these numbers include

where {{math|γ {{=}} 0.5772156649...}} is Euler's constant. These results are very old, and their history may be traced back to the works of Gregorio Fontana and Lorenzo Mascheroni.[15][20] More complicated series with the Gregory coefficients were calculated by various authors. Kowalenko,[6] Alabdulmohsin [10][11] and some other authors calculated

Alabdulmohsin[21][22] also gives these identities

Candelperger, Coppo[23][24] and Young[5] showed that

where {{math|Hn}} are the harmonic numbers.

Blagouchine[15][25][26][27] provides the following identities

where {{math|li(z)}} is the integral logarithm and 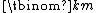is the binomial coefficient.

It is also known that the zeta function, the gamma function, the polygamma functions, the Stieltjes constants and many other special functions and constants may be expressed in terms of infinite series containing these numbers.[1][15][16][28][29]

Generalizations

Various generalizations are possible for the Gregory coefficients. Many of them may be obtained by modifying the parent generating equation. For example, Van Veen[16] consider

and hence

Equivalent generalizations were later proposed by Kowalenko[7] and Rubinstein.[30] In a similar manner, Gregory coefficients are related to the generalized Bernoulli numbers

see,[16][28] so that

Jordan[1][19][31] defines polynomials {{math|ψn(s)}} such that

and call them Bernoulli polynomials of the second kind. From the above, it is clear that {{math|Gn {{=}} ψn(0)}}.

Carlitz[32] generalized Jordan's polynomials {{math|ψn(s)}} by introducing polynomials {{math|β}}

and therefore

Blagouchine[15][33] introduced numbers {{math|Gn(k)}} such that

obtained their generating function and studied their asymptotics at large {{math|n}}. Clearly, {{math|Gn {{=}} Gn(1)}}. These numbers are strictly alternating {{math|Gn(k) {{=}} (-1)n-1{{!}}Gn(k){{!}}}} and involved in various expansions for the zeta-functions, Euler's constant and polygamma functions.

A different generalization of the same kind was also proposed by Komatsu[31]

so that {{math|Gn {{=}} cn(1)/n!}} Numbers {{math|cn(k)}} are called by the author poly-Cauchy numbers.[31] Coffey[18]

defines polynomials

and therefore {{math|{{!}}Gn{{!}} {{=}} Pn+1(1)}}.

See also

  • Stirling polynomials
  • Bernoulli polynomials of the second kind

References

1. ^1 2 3 Ch. Jordan. The Calculus of Finite Differences Chelsea Publishing Company, USA, 1947.
2. ^1 L. Comtet. Advanced combinatorics (2nd Edn.) D. Reidel Publishing Company, Boston, USA, 1974.
3. ^P. C. Stamper. Table of Gregory coefficients. Math. Comp. vol. 20, p. 465, 1966.
4. ^1 D. Merlini, R. Sprugnoli, M. C. Verri. The Cauchy numbers. Discrete Math., vol. 306, pp. 1906–1920, 2006.
5. ^1 P.T. Young. A 2-adic formula for Bernoulli numbers of the second kind and for the Nörlund numbers. J. Number Theory, vol. 128, pp. 2951–2962, 2008.
6. ^1 [https://link.springer.com/article/10.1007%2Fs10440-008-9325-0 V. Kowalenko. Properties and Applications of the Reciprocal Logarithm Numbers. Acta Appl. Math., vol. 109, pp. 413–437, 2010.]
7. ^1 [https://link.springer.com/article/10.1007%2Fs10440-008-9304-5 V. Kowalenko. Generalizing the reciprocal logarithm numbers by adapting the partition method for a power series expansion. Acta Appl. Math., vol. 106, pp. 369–420, 2009.]
8. ^I. Mezo. Gompertz Constant, Gregory Coefficients and a Series of the Logarithm Function. J. Ana. Num. Theor. 2, No. 2, pp. 33–36, 2014.
9. ^F. Qi and X.-J. Zhang An integral representation, some inequalities, and complete monotonicity of Bernoulli numbers of the second kind. Bull. Korean Math. Soc., vol. 52, no. 3, pp. 987–98, 2015.
10. ^Weisstein, Eric W. "Logarithmic Number." From MathWorld—A Wolfram Web Resource.
11. ^1 J.F. Steffensen. Interpolation (2nd Edn.). Chelsea Publishing Company, NewYork, USA, 1950.
12. ^1 J. C. Kluyver. Euler's constant and natural numbers. Proc. K. Ned. Akad. Wet., vol. 27(1-2), 1924.
13. ^1 I. V. Blagouchine, [https://cs.uwaterloo.ca/journals/JIS/VOL20/Blagouchine/blag5.html A Note on Some Recent Results for the Bernoulli Numbers of the Second Kind, Journal of Integer Sequences, Vol. 20, No. 3 (2017), Article 17.3.8] [https://arxiv.org/abs/1612.03292 arXiv:1612.03292]
14. ^Ernst Schröder, Zeitschrift fur Mathematik und Physik, vol. 25, pp. 106–117 (1880)
15. ^1 2 3 4 5 6 7 [https://dx.doi.org/10.1016/j.jmaa.2016.04.032 Ia.V. Blagouchine. Two series expansions for the logarithm of the gamma function involving Stirling numbers and containing only rational coefficients for certain arguments related to {{pi}}−1. J.Math. Anal. Appl., 2015.]
16. ^1 2 3 4 S.C. Van Veen. Asymptotic expansion of the generalized Bernoulli numbers Bn(n − 1) for large values of n (n integer). Indag. Math. (Proc.), vol. 13, pp. 335–341, 1951.
17. ^1 [https://www.jstor.org/stable/2308510 H.T. Davis. The approximation of logarithmic numbers. Amer. Math. Monthly, vol. 64, no. 8, pp. 11–18, 1957.]
18. ^1 [https://projecteuclid.org/euclid.rmjm/1407154909 M.W. Coffey. Series representations for the Stieltjes constants. Rocky Mountain J. Math., vol. 44, pp. 443–477, 2014.]
19. ^1 G. Nemes. An asymptotic expansion for the Bernoulli numbers of the second kind. J. Integer Seq, vol. 14, 11.4.8, 2011
20. ^Ia.V. Blagouchine. A theorem for the closed-form evaluation of the first generalized Stieltjes constant at rational arguments and some related summations J. Number Theory, vol. 148, pp. 537–592 and vol. 151, pp. 276–277, 2015.
21. ^1 2 [https://arxiv.org/abs/1209.5739 I. M. Alabdulmohsin. Summability calculus, arXiv:1209.5739, 2012.]
22. ^1 2 [https://www.springer.com/gp/book/9783319746470 I. M. Alabdulmohsin. Summability calculus: a Comprehensive Theory of Fractional Finite Sums, Springer International Publishing, 2018.]
23. ^[https://link.springer.com/article/10.1007%2Fs11139-011-9361-7 B. Candelpergher and M.-A. Coppo. A new class of identities involving Cauchy numbers, harmonic numbers and zeta values. Ramanujan J., vol. 27, pp. 305–328, 2012.]
24. ^[https://hal.inria.fr/file/index/docid/634313/filename/ArtZetamod.pdf B. Candelpergher and M.-A. Coppo. A new class of identities involving Cauchy numbers, harmonic numbers and zeta values. Ramanujan J., vol. 27, pp. 305–328, 2012]
25. ^{{OEIS2C|id=A269330}}
26. ^{{OEIS2C|id=A270857}}
27. ^{{OEIS2C|id=A270859}}
28. ^1 N. Nörlund. Vorlesungen über Differenzenrechnung. Springer, Berlin, 1924.
29. ^Ia.V. Blagouchine. Expansions of generalized Euler's constants into the series of polynomials in {{pi}}−2 and into the formal enveloping series with rational coefficients only J. Number Theory, vol. 158, pp. 365–396, 2016.
30. ^[https://link.springer.com/article/10.1007%2Fs11139-010-9276-8 M. O. Rubinstein. Identities for the Riemann zeta function Ramanujan J., vol. 27, pp. 29–42, 2012.]
31. ^1 2 [https://carma.newcastle.edu.au/alfcon/pdfs/Takao_Komatsu-alfcon.pdf Takao Komatsu. On poly-Cauchy numbers and polynomials, 2012.]
32. ^1 2 L. Carlitz. A note on Bernoulli and Euler polynomials of the second kind. Scripta Math., vol. 25, pp. 323–330,1961.
33. ^Ia.V. Blagouchine. Three Notes on Ser's and Hasse's Representations for the Zeta-functions Integers (Electronic Journal of Combinatorial Number Theory), vol. 18A, Article #A3, pp. 1–45, 2018. [https://arxiv.org/abs/1606.02044 arXiv:1606.02044]

4 : Integer sequences|Number theory|Inequalities|Asymptotic analysis
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/12 16:00:45