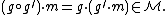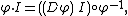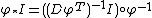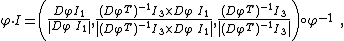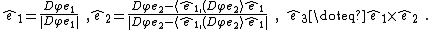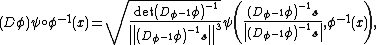- The orbit model of computational anatomy
- Several group actions in computational anatomy Submanifolds: organs, subcortical structures, charts, and immersions Scalar images such as MRI, CT, PET Oriented tangents on curves, eigenvectors of tensor matrices Tensor matrices Orientation Distribution Function and High Angular Resolution HARDI
- References
Group actions are central to Riemannian geometry and defining orbits (control theory).
The orbits of computational anatomy consist of anatomical shapes and medical images; the anatomical shapes are submanifolds of differential geometry
This generalized the ideas of the more familiar orbits of linear algebra which are linear vector spaces. Medical images are scalar and tensor images from medical imaging. The group actions are used to define models of human shape which accommodate variation. These orbits are deformable templates as originally formulated more abstractly in pattern theory.
The orbit model of computational anatomy
The central model of human anatomy in computational anatomy is a Groups and group action, a classic formulation from differential geometry. The orbit is called the space of shapes and forms.[1] The space of shapes are denoted 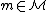 , with the group
, with the group  with law of composition
with law of composition  ; the action of the group on shapes is denoted
; the action of the group on shapes is denoted 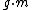 , where the action of the group
, where the action of the group 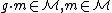 is defined to satisfy
is defined to satisfy
The orbit  of the template becomes the space of all shapes,
of the template becomes the space of all shapes, 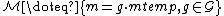 .
.
Several group actions in computational anatomy
{{Main|Computational anatomy}}The central group in CA defined on volumes in 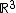 are the diffeomorphism group
are the diffeomorphism group 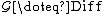 which are mappings with 3-components
which are mappings with 3-components 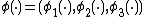 , law of composition of functions
, law of composition of functions  , with inverse
, with inverse 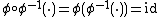 .
.
Submanifolds: organs, subcortical structures, charts, and immersions
For sub-manifold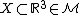 , parametrized by a chart or immersion
, parametrized by a chart or immersion 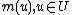 , the diffeomorphic action the flow of the position
, the diffeomorphic action the flow of the position
.
Scalar images such as MRI, CT, PET
Most popular are scalar images, 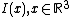 , with action on the right via the inverse.
, with action on the right via the inverse.
.
Oriented tangents on curves, eigenvectors of tensor matrices
Many different imaging modalities are being used with various actions. For images such that  is a three-dimensional vector then
is a three-dimensional vector then
Tensor matrices
Cao et al.
[2]examined actions for mapping MRI images measured via diffusion tensor imaging and represented via there principle eigenvector.
For tensor fields a positively oriented orthonormal basis
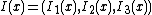
of 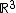 , termed frames, vector cross product denoted
, termed frames, vector cross product denoted 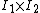 then
then
The Fr\\'enet frame of three orthonormal vectors,  deforms as a tangent,
deforms as a tangent, 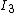 deforms like
deforms like
a normal to the plane generated by 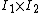 , and
, and 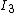 . H is uniquely constrained by the
. H is uniquely constrained by the
basis being positive and orthonormal.
For 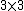 non-negative symmetric matrices, an action would become
non-negative symmetric matrices, an action would become 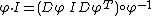 .
.
For mapping MRI DTI images[3][4] (tensors), then eigenvalues are preserved with the diffeomorphism rotating eigenvectors and preserves the eigenvalues.
Given eigenelements
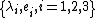 , then the action becomes
, then the action becomes
Orientation Distribution Function and High Angular Resolution HARDI
{{Further|Computational_anatomy#Diffusion_tensor_image_matching_in_computational_anatomy|LDDMM#LDDMM ODF}}Orientation distribution function (ODF) characterizes the angular profile of the diffusion probability density function of water molecules and can be reconstructed from High Angular Resolution Diffusion Imaging (HARDI). The ODF is a probability density function defined on a unit sphere, 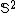 . In the field of information geometry,[5] the space of ODF forms a Riemannian manifold with the Fisher-Rao metric. For the purpose of LDDMM ODF mapping, the square-root representation is chosen because it is one of the most efficient representations found to date as the various Riemannian operations, such as geodesics, exponential maps, and logarithm maps, are available in closed form. In the following, denote square-root ODF (
. In the field of information geometry,[5] the space of ODF forms a Riemannian manifold with the Fisher-Rao metric. For the purpose of LDDMM ODF mapping, the square-root representation is chosen because it is one of the most efficient representations found to date as the various Riemannian operations, such as geodesics, exponential maps, and logarithm maps, are available in closed form. In the following, denote square-root ODF (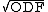 ) as
) as 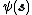 , where
, where 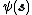 is non-negative to ensure uniqueness and
is non-negative to ensure uniqueness and 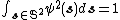 .
.
Denote diffeomorphic transformation as  . Group action of diffeomorphism on
. Group action of diffeomorphism on 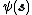 ,
, 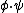 , needs to guarantee the non-negativity and
, needs to guarantee the non-negativity and 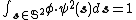 . Based on the derivation in,[6] this group action is defined as
. Based on the derivation in,[6] this group action is defined as
where 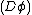 is the Jacobian of
is the Jacobian of  .
.
References
2. ^Cao Y1, Miller MI, Winslow RL, Younes, Large deformation diffeomorphic metric mapping of vector fields. IEEE Trans Med Imaging. 2005 Sep;24(9):1216-30.
3. ^{{Cite journal|title = Spatial transformations of diffusion tensor magnetic resonance images|journal = IEEE Transactions on Medical Imaging|date = 2001-11-01|issn = 0278-0062|pmid = 11700739|pages = 1131–1139|volume = 20|issue = 11|doi = 10.1109/42.963816|first = D. C.|last = Alexander|first2 = C.|last2 = Pierpaoli|first3 = P. J.|last3 = Basser|first4 = J. C.|last4 = Gee}}
4. ^{{Cite book|title = Diffeomorphic Matching of Diffusion Tensor Images|journal = Proceedings / CVPR, IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE Computer Society Conference on Computer Vision and Pattern Recognition|date = 2006-07-05|issn = 1063-6919|pmc = 2920614|pmid = 20711423|pages = 67|volume = 2006|doi = 10.1109/CVPRW.2006.65|first = Yan|last = Cao|first2 = Michael I.|last2 = Miller|first3 = Susumu|last3 = Mori|first4 = Raimond L.|last4 = Winslow|first5 = Laurent|last5 = Younes|isbn = 978-0-7695-2646-1}}
5. ^{{cite book|last1=Amari|first1=S|title=Differential-Geometrical Methods in Statistics|date=1985|publisher=Springer}}
6. ^{{cite journal|last1=Du|first1=J|last2=Goh|first2=A|last3=Qiu|first3=A|title=Diffeomorphic metric mapping of high angular resolution diffusion imaging based on Riemannian structure of orientation distribution functions|journal=IEEE Trans Med Imaging|date=2012|volume=31|issue=5|pages=1021–1033|doi=10.1109/TMI.2011.2178253|pmid=22156979}}
- Draft:Dynasty Capital Management
- Draft:Dynasty (season 1)
- Draft:Dynasty (season 2)
- Draft:Dynasty (season 3)
- Draft:DynaSys
- Draft:DynaSys, a Division of QAD
- Draft:Dyron Miller
- Draft:DYRY
- Draft:Dyscourse
- Draft:Dysdera castillonensis
- Draft:Dyson College of Arts and Sciences
- Draft:Dyson electric car
- Draft:DZCT
- Draft:DZEA
- Draft:Dzhokhar Dudayev Battalion
- Draft:Dzianis Krytski
- Draft:Dziun
- Draft:DZJC
- Draft:DZZB-TV
- Draft:DÖVLƏT VƏ İCTİMAİ MÜNASİBƏTLƏR FAKULTƏSİ
- Draft:Dénes König Prize
- Draft:Désiré Tsarahazana
- Draft:Désobéissance
- Draft:Développement Tous Azimuts (DTA)
- Draft:Dípò Awojide