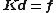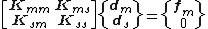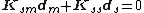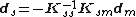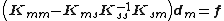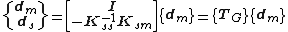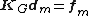“Guyan reduction”的意思、由来-开放百科全书

词条

Guyan reduction

释义

Basic concept
Linear transformation
See also
References

In computational mechanics, Guyan reduction, also known as static condensation, is a dimensionality reduction method which reduces the number of degrees of freedom by ignoring the inertial terms of the equilibrium equations and expressing the unloaded degrees of freedom in terms of the loaded degrees of freedom.

Basic concept

The static equilibrium equation can be expressed as:

where is the stiffness matrix, 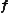the force vector, and the displacement vector. The number of the degrees of freedom of the static equilibrium problem is the length of the displacement vector.

By partitioning the above system of linear equations with regards to loaded (master) and unloaded (slave) degrees of freedom, the static equilibrium equation may be expressed as:

where represents the zero vector.

Focusing on the lower partition of the above system of linear equations, the dependent (slave) degrees of freedom are expressed by the following equation.

Solving the above equation in terms of the independent (master) degrees of freedom leads to the following dependency relations

Substituting the dependency relations on the upper partition of the static equilibrium problem condenses away the slave degrees of freedom, leading to the following reduced system of linear equations.

The above system of linear equations is equivalent to the original problem, but expressed in terms of the master degrees of freedom alone.

Thus, the Guyan reduction method results in a reduced system by condensing away the slave degrees of freedom.

Linear transformation

The Guyan reduction can also be expressed as a change of basis which produces a low-dimensional representation of the original space, represented by the master degrees of freedom.

The linear transformation that maps the reduced space onto the full space is expressed as:

where 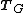represents the Guyan reduction transformation matrix.

Thus, the reduced problem is represented as:

In the above equation, 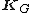represents the reduced system of linear equations that's obtained by applying the Guyan reduction transformation on the full system, which is expressed as:

References

2 : Finite element method|Structural analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Basic concept

Linear transformation

See also

References