“Heilbronn set”的意思、由来-开放百科全书

In mathematics, a Heilbronn set is an infinite set S of natural numbers for which every real number can be arbitrarily closely approximated by a fraction whose denominator is in S. For any given real number

and natural number

, it is easy to find the integer

such that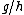

is closest to

. For example, for the real number

and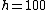

we have

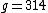. If we call the closeness of

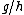the difference between

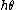and

, the closeness is always less than 1/2 (in our example it is 0.15926...). A collection of numbers is a Heilbronn set if for any

we can always find a sequence of values for

in the set where the closeness tends to zero.

More mathematically let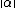

denote the distance from

to the nearest integer then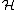

is a Heilbronn set if and only if for every real number

and every

there exists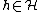

such that

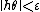.^[1]

Examples

The natural numbers are a Heilbronn set as Dirichlet's approximation theorem shows that there exists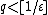

with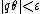

The

th powers of integers are a Heilbronn set. This follows from a result of I. M. Vinogradov who showed that for every

and

there exists an exponent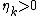

and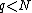

such that

.^[2] In the case

Hans Heilbronn was able to show that

may be taken arbtrarily close to 1/2.^[3] Alexandru Zaharescu has improved Heilbronn's result to show that

may be taken arbitrarily close to 4/7.^[4]

Example of a non-Heilbronn set

The powers of 10 are not a Heilbronn set. Take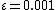

then the statement that

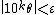for some

is equivalent to saying that the decimal expansion of

has run of three zeros or three nines somewhere. This is not true for all real numbers.

References

1. ^{{cite book | first=Hugh Lowell | last=Montgomery |authorlink =Hugh Lowell Montgomery | title=Ten lectures on the Interface Between Analytic Number Theory and Harmonic Analysis| volume=84 | series=CBMS Regional Conference Series in Mathematics | year=1994 | publisher=American Mathematical Society | location=Providence Rhode Island | isbn=0-8218-0737-4 }}
2. ^{{cite journal |first=I. M. |last=Vinogradov |authorlink= I. M. Vinogradov | title= Analytischer Beweis des Satzes uber die Verteilung der Bruchteile eines ganzen Polynoms |year= 1927| volume=21| issue=6 | pages=567−578 | journal=Bull. Acad. Sci. USSR}}
3. ^{{cite journal |first=Hans|last=Heilbronn|authorlink = Hans Heilbronn |title= On the distribution of the sequence

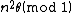|year= 1948| volume=19 | pages=249−256 | journal=Quart. J. Math., Oxford Ser.|mr=0027294}}
4. ^{{cite journal |first=Alexandru |last=Zaharescu|authorlink = Alexandru Zaharescu|title= Small values of

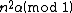|year= 1995| volume=121| issue=2 | pages=379−388 | journal=Invent. Math.|mr=1346212}}