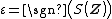| 释义 |
Planar rotations with complex, hyperbolic, and dual numbers Comparing complex, hyperbolic and dual numbers - Definition
- Character and type of a hybrid number
- Norms of hybrid numbers
- Inverse of a hybrid number
- Argument of a hybrid number
- Polar form of a hybrid number
- De Moivre's formulas for hybrid numbers
- Roots of a hybrid number
- The matrix representation of hybrid numbers
- The logarithm of a hybrid number
- Euler's formulas for the hybrid numbers
- See also
- References
|+Hybrid multiplication |- !width=15|× !width=15| !width=15|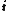 !width=15| !width=15|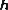 |- ! | |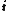 | |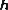 |- !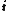 |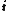 |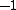 | |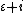 |- ! | |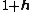 | | |- !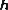 |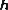 |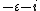 | | |} A hybrid number is a generalization of complex numbers 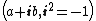 , split-complex numbers (or "hyperbolic number") , split-complex numbers (or "hyperbolic number") 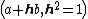 and dual numbers and dual numbers 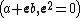 . Hybrid numbers form a noncommutative ring. Complex, hyperbolic and dual numbers are well known two-dimensional number systems. It is well known that, the set of complex numbers, hyperbolic numbers and dual numbers are . Hybrid numbers form a noncommutative ring. Complex, hyperbolic and dual numbers are well known two-dimensional number systems. It is well known that, the set of complex numbers, hyperbolic numbers and dual numbers are 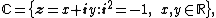
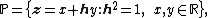
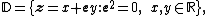
respectively. The algebra of hybrid numbers is a noncommutative algebra which unifies all three number systems calls them hybrid numbers.[1], [2], [3]. A hybrid number 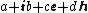
is a number created with any combination of the complex, hyperbolic and dual numbers satisfying the relation 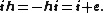
Because these numbers are a composition of dual, complex and hyperbolic numbers, Ozdemir calls them hybrid numbers [4]. A commutative two-dimensional unital algebra generated by a 2 by 2 matrix is isomorphic to either complex, dual or hyperbolic numbers [5]. Due to the set of hybrid numbers is a two-dimensional commutative algebra spanned by 1 and 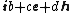 , it is isomorphic to one of the complex, dual or hyperbolic numbers. , it is isomorphic to one of the complex, dual or hyperbolic numbers. Planar rotations with complex, hyperbolic, and dual numbers Especially in the last century, a lot of researchers deal with the geometric and physical applications of these numbers. Just as the geometry of the Euclidean plane can be described with complex numbers, the geometry of the Minkowski plane and Galilean plane can be described with hyperbolic numbers. The group of Euclidean rotations SO(2) is isomorphic to the group U(1) of unit complex numbers. The geometrical meaning of multiplying by 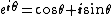 means a rotation of the plane. [6], [7]. means a rotation of the plane. [6], [7].
The group of Lorentzian rotations 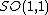 is isomorphic to the group of unit spacelike hyperbolic numbers. This rotation can be viewed as hyperbolic rotation. Thus, multiplying by is isomorphic to the group of unit spacelike hyperbolic numbers. This rotation can be viewed as hyperbolic rotation. Thus, multiplying by 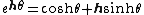 means a map of hyperbolic numbers into itself which preserves the Lorentzian metric. [8], [9], means a map of hyperbolic numbers into itself which preserves the Lorentzian metric. [8], [9], [10], [11]The Galilean rotations can be interpreted with dual numbers. The concept of a rotation in the dual number plane is equivalent to a vertical shear mapping since 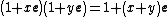 . The Euler formula for dual numbers is . The Euler formula for dual numbers is  . Multiplying by . Multiplying by 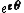 is a is a
map of dual numbers into itself which preserves the Galilean metric. This rotation can be named as parabolic rotation [12], [13][14][15], [16], [17], [18], [19]. In abstract algebra, the complex, the hyperbolic and the dual numbers can be described as the quotient of the polynomial ring  by the ideal generated by the polynomials by the ideal generated by the polynomials 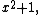 , , 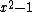 and and 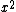 respectively. That is, respectively. That is,
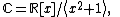 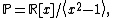 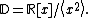 Matrix represantations of the units 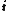 , ,  , , 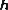 are are 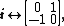 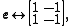 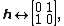
respectively. Comparing complex, hyperbolic and dual numbers |- ! Properties !! Complex numbers !! Hyperbolic numbers !! Dual numbers |- | Algebraic structure || Field || Commutative ring || Commutative ring |- | Property || 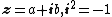 || || 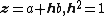 || ||  |- | Conjugate || 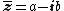 || || 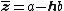 || || 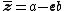 |- | Norm ||  || || 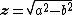 || ||  |- | Geometry || Euclidean geometry || Lorentzian geometry || Galilean geometry |- | Circle || 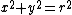 || || 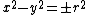 || ||  |- | Rotation type || Elliptic rotation || Hyperbolic rotation || Parabolic rotation |- | Euler's Formula || 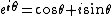 || || 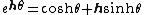 || || 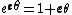 |- | Argument ||  || || 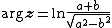 || || 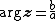 |} Definition The set of hybrid numbers  , defined as , defined as 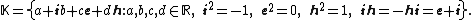 For the hybrid number 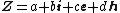 , the number , the number  is called the scalar part and is denoted by is called the scalar part and is denoted by 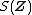 ; ; 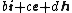 is called the vector part and is denoted by is called the vector part and is denoted by 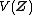 [20]The conjugate of a hybrid number 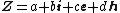 , denoted by , denoted by 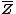 , is , is defined as 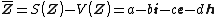 as in as in quaternions. Multiplication operation in the hybrid numbers is associative and not commutative. Let 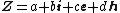 be a hybrid number. The real number be a hybrid number. The real number 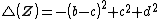
is called the type number of 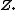 We say that a hybrid number; We say that a hybrid number; 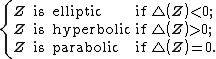
These are called the \\textbf{types of the hybrid numbers}. The vector 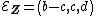 is called hybridian vector of is called hybridian vector of 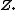 Norms of hybrid numbers Let 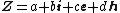 be a hybrid number. The real number be a hybrid number. The real number 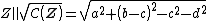
is called the norm of 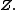 Besides, the real number Besides, the real number 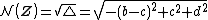
will be called the norm of the hybrid vector of  . This norm definition is a generalized norm definition that overlaps with the definitions of norms in complex, hyperbolic and dual numbers. . This norm definition is a generalized norm definition that overlaps with the definitions of norms in complex, hyperbolic and dual numbers. - If
 is a complex number is a complex number 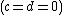 , then , then 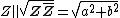
- If
 is a hyperbolic number is a hyperbolic number 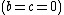 , then , then 
- If
 is a dual number is a dual number 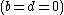 , then , then 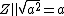 . .
Inverse of a hybrid number Using the hybridian product of hybrid numbers, one can show that the equality 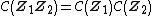 holds So, holds So, timelike hybrid numbers form a group according to the multiplication operation. The inverse of a hybrid number 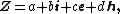 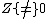 is defined as is defined as 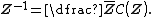
Accordingly, lightlike hybrid numbers have no inverse. Argument of a hybrid number Let 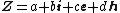 be a be a hybrid number. The argument 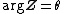 of of  is defined as follows with respect is defined as follows with respect to its type. 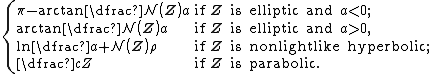
Polar form of a hybrid number Let 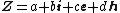 be a hybrid number, and be a hybrid number, and 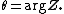 i. If  is elliptic, then is elliptic, then 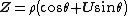 such that such that 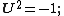 ii. If  a lightlike hyperbolic, then a lightlike hyperbolic, then 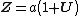 such that such that 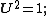 iii. If  is spacelike or timelike hyperbolic, then, is spacelike or timelike hyperbolic, then, 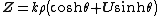 such that such that 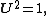 where where 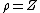 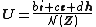 and and  for 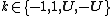 iv. If  is a parabolic hybrid number, then is a parabolic hybrid number, then 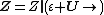 where where 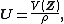 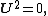 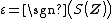 . . De Moivre's formulas for hybrid numbers De Moivre's formula for hybrid numbers as follows..[21]. Let 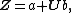 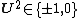 be a spacelike or timelike hybrid be a spacelike or timelike hybrid number. If  and and 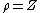 i. If  is elliptic, then is elliptic, then 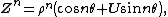 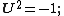 ii. If  is hyperbolic, then is hyperbolic, then 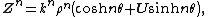 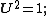 iii. If  is parabolic, then is parabolic, then  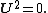 If 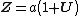 is a lightlike hybrid number, then is a lightlike hybrid number, then 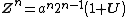 where where 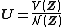 and and 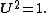 Roots of a hybrid number Let  be a hybrid number and be a hybrid number and 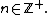 The hybrid numbers The hybrid numbers  satisfying the equation satisfying the equation 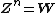 can be found as follows can be found as follows [22], [3]i. If 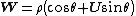 is an elliptic hybrid number, then the roots of is an elliptic hybrid number, then the roots of  are in the form are in the form 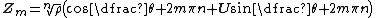
for 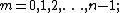 ii. If 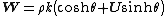 is a spacelike or timelike hyperbolic hybrid number, then the roots of is a spacelike or timelike hyperbolic hybrid number, then the roots of  are in the form are in the form 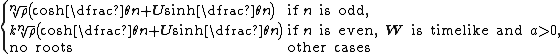
where 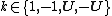 ; ; iii. If 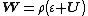 , , 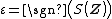 is a parabolic hybrid number, the only root is is a parabolic hybrid number, the only root is  where 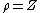 If 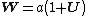 is a lightlike hybrid number, then is a lightlike hybrid number, then 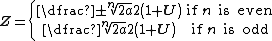
for 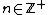 where where 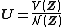 and and 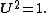 The matrix representation of hybrid numbers Just as complex numbers and quaternions can be represented as matrices, so can hybrid numbers. There are at least two ways of representing hybrid numbers as real matrices in such a way that hybrid addition and multiplication correspond to matrix addition and matrix multiplication. The hybrid number ring  is isomorphic to is isomorphic to 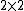 matrix rings matrix rings 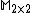 . . So, each hybrid number can be represented by a 2 by 2 real matrix. Thus, it can be done operations and calculations in the hybrid numbers using the corresponding matrices.[23][3][24] The map  is a ring isomorphism where is a ring isomorphism where 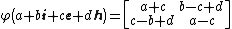
for 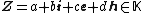 . .
Also, the real matrix 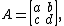
corresponds to the hybrid number 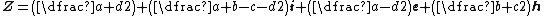
According to this ring isomorphism, matrix represantations of the units 1, 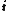 , ,  , , 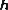 are as follows : are as follows :
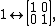 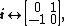 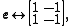 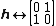 Let  be a 2 by 2 real matrix corresponding to the hybrid number be a 2 by 2 real matrix corresponding to the hybrid number 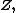 then there are the following equalities. then there are the following equalities. -
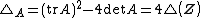 is discriminant of the characteristic polynomial of is discriminant of the characteristic polynomial of 
-
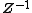 exists if and only if exists if and only if 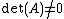 . .
|- ! Type of hybrid number !! Euler formula |- |  is timelike hyperbolic || is timelike hyperbolic || 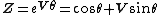 |- |  is spacelike hyperbolic || is spacelike hyperbolic || 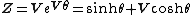 |- | is parabolic || is parabolic || 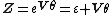 , , 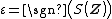 |} See also{{Div col|colwidth=20em}}- Associative algebra
- Complex number
- Biquaternion
- Clifford algebra
- Complex number
- Conversion between quaternions and Euler angles
- Division algebra
- Dual number
- Dual quaternion
- Euler angles
- Exterior algebra
- Geometric algebra
- Hyperbolic quaternion
- Hypercomplex number
- Octonion
- Pauli matrices
- Quaternion
- Quaternion variable
- Quaternionic matrix
- Quaternions and spatial rotation
- Rotations in 4-dimensional Euclidean space
- Split-quaternion
{{Div col end}} References 1. ^{{cite journal | last1 = Ozdemir | first1 = M. | title = Introduction to Hybrid Numbers | journal = Applied Clifford Algebras | volume = 28:11, 2018.| doi = 10.1007/s00006-018-0833-3 | year = 2018 }}
2. ^G. Dattoli, S. Licciardi, R. M. Pidatella, E. Sabia, Hybrid Complex Numbers: The Matrix Version, Adv. in Applied Clifford Algebras, 28:58, (2018)
3. ^1 2 Özdemir M., Finding n-th Roots of a 2×2 Real Matrix Using De Moivre's Formula, Adv. in Applied Clifford Algebras, 29:2, (2019)
4. ^{{cite journal | last1 = Ozdemir | first1 = M. | title = Introduction to Hybrid Numbers | journal = Applied Clifford Algebras | volume = 28:11, 2018.| doi = 10.1007/s00006-018-0833-3 | year = 2018 }}
5. ^Lavrentiev M.A., Shabat B.V., Problems of hydrodynamics and their mathematical models. Moscow, Nauka, 416 p., (Russian) (1973).
6. ^Yaglom I.M., Complex Numbers in Geometry, Academic Press, (1968).
7. ^Yaglom I.M., A simple non-Euclidean geometry and its physical basis. Heidelberg Science Library. Springer-Verlag, New York, (1979).
8. ^Catoni F., Cannata R., Catoni V., Zampetti P., Two-dimensional Hypercomplex number and related trigonometries, Advances in Applied Clifford Algebras, Vol.14, Issue 1, 47–68, (2004).
9. ^Catoni F., Boccaletti D.,Cannata R., Catoni V., Nichelatti E., and Zampetti P., The Mathematics of Minkowski Space-Time: With an Introduction to Commutative Hypercomplex Numbers, Birkhäuser, Basel, (2008).
10. ^ Catoni F., Cannata R., Catoni V., Zampetti P.: Hyperbolic trigonometry in two-dimensional space-time geometry. Nuovo Cimento B, 118(5), 475 (2003).
11. ^Rooney J., On the three types of complex number and planar transformations, Environment and Planning B, Volume 5, pages 89–99, (1978).
12. ^Kisil Vladimir V., Induced Representations and Hypercomplex Numbers, Advances in Applied Clifford Algebras, Vol.23, Issue 2, pp 417–440, (2013)
13. ^Kisil Vladimir V., Erlangen program at large-2: Inventing a wheel. The parabolic one. Trans. Inst. Math. of the NAS of Ukraine, pages 89–98, (2010).
14. ^Kisil Vladimir V., Erlangen program at large-1: Geometry of invariants. SIGMA, Symmetry Integrability Geom. Methods Appl. 6 (076):45, (2010).
15. ^Rooney J., Generalised Complex Numbers in Mechanics, Advances on Theory and Practice of Robots and Manipulators, 55–62, (2014).
16. ^Harkin A. A., Harkin J. B., Geometry of Generalized Complex Numbers, Mathematics Magazine 77(2):118–29 (2004)
17. ^Fischer I., Dual-Number Methods in Kinematics, Statics and Dynamics. CRC Press, (1999).
18. ^Borota N. A., Flores E., and Osler T.J., Spacetime numbers the easy way, Mathematics and Computer Education 34: 159–168 (2000).
19. ^Veldkamp G.R., On the use of dual numbers, vectors and matrices in instantaneous, spatial kinematics, Mechanism and Machine Theory, Volume 11, Issue 2, pages 141–156, (1976)
20. ^{{cite journal | last1 = Ozdemir | first1 = M. | title = Introduction to Hybrid Numbers | journal = Applied Clifford Algebras | volume = 28:11, 2018.| doi = 10.1007/s00006-018-0833-3 | year = 2018 }}
21. ^{{cite journal | last1 = Ozdemir | first1 = M. | title = Introduction to Hybrid Numbers | journal = Applied Clifford Algebras | volume = 28:11, 2018.| doi = 10.1007/s00006-018-0833-3 | year = 2018 }}
22. ^{{cite journal | last1 = Ozdemir | first1 = M. | title = Introduction to Hybrid Numbers | journal = Applied Clifford Algebras | volume = 28:11, 2018.| doi = 10.1007/s00006-018-0833-3 | year = 2018 }}
23. ^{{cite journal | last1 = Ozdemir | first1 = M. | title = Introduction to Hybrid Numbers | journal = Applied Clifford Algebras | volume = 28:11, 2018.| doi = 10.1007/s00006-018-0833-3 | year = 2018 }}
24. ^G. Dattoli, S. Licciardi, R. M. Pidatella, E. Sabia, Hybrid Complex Numbers: The Matrix Version, Adv. in Applied Clifford Algebras, 28:58, (2018)
{{Number systems}} 1 : Complex numbers
| 随便看 |
|
开放百科全书收录14589846条英语、德语、日语等多语种百科知识,基本涵盖了大多数领域的百科知识,是一部内容自由、开放的电子版国际百科全书。
|

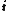

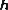
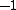

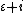
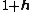


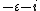

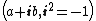 , split-complex numbers (or "hyperbolic number")
, split-complex numbers (or "hyperbolic number") 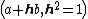 and dual numbers
and dual numbers 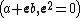 . Hybrid numbers form a noncommutative ring. Complex, hyperbolic and dual numbers are well known two-dimensional number systems. It is well known that, the set of complex numbers, hyperbolic numbers and dual numbers are
. Hybrid numbers form a noncommutative ring. Complex, hyperbolic and dual numbers are well known two-dimensional number systems. It is well known that, the set of complex numbers, hyperbolic numbers and dual numbers are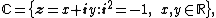
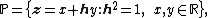
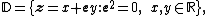
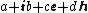
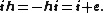
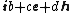 , it is isomorphic to one of the complex, dual or hyperbolic numbers.
, it is isomorphic to one of the complex, dual or hyperbolic numbers.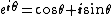 means a rotation of the plane. [6], [7].
means a rotation of the plane. [6], [7].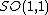 is isomorphic to the group of unit spacelike hyperbolic numbers. This rotation can be viewed as hyperbolic rotation. Thus, multiplying by
is isomorphic to the group of unit spacelike hyperbolic numbers. This rotation can be viewed as hyperbolic rotation. Thus, multiplying by 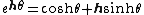 means a map of hyperbolic numbers into itself which preserves the Lorentzian metric. [8], [9],
means a map of hyperbolic numbers into itself which preserves the Lorentzian metric. [8], [9],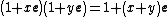 . The Euler formula for dual numbers is
. The Euler formula for dual numbers is  . Multiplying by
. Multiplying by 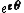 is a
is a by the ideal generated by the polynomials
by the ideal generated by the polynomials 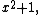 ,
, 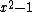 and
and 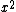 respectively. That is,
respectively. That is,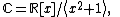
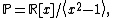
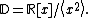
 ,
, 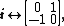
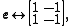
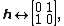
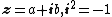 ||
|| 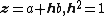 ||
|| 
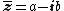 ||
|| 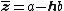 ||
|| 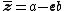
 ||
|| 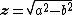 ||
|| 
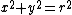 ||
|| 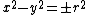 ||
|| 
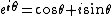 ||
|| 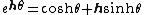 ||
|| 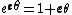
 ||
|| 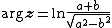 ||
|| 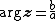
 , defined as
, defined as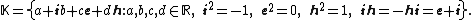
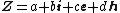 , the number
, the number  is called the scalar part and is denoted by
is called the scalar part and is denoted by 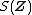 ;
; 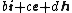 is called the vector part and is denoted by
is called the vector part and is denoted by 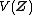
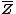 , is
, is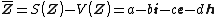 as in
as in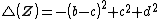
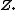 We say that a hybrid number;
We say that a hybrid number;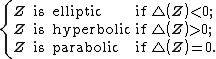
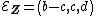 is called hybridian vector of
is called hybridian vector of 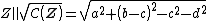
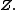 Besides, the real number
Besides, the real number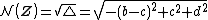
 . This norm definition is a generalized norm definition that overlaps with the definitions of norms in complex, hyperbolic and dual numbers.
. This norm definition is a generalized norm definition that overlaps with the definitions of norms in complex, hyperbolic and dual numbers.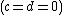 , then
, then 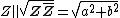
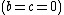 , then
, then 
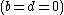 , then
, then 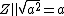 .
.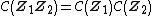 holds So,
holds So,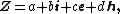
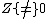 is defined as
is defined as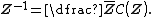
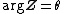 of
of 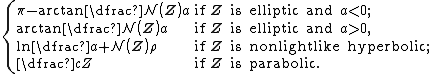
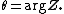
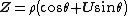 such that
such that 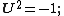
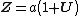 such that
such that 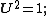
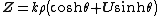 such that
such that 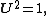 where
where 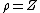
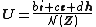 and
and
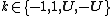
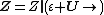 where
where 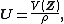
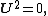
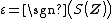 .
.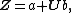
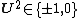 be a spacelike or timelike hybrid
be a spacelike or timelike hybrid and
and 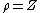
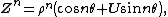
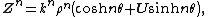

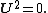
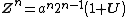 where
where 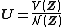 and
and 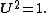
 be a hybrid number and
be a hybrid number and 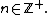 The hybrid numbers
The hybrid numbers 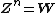 can be found as follows
can be found as follows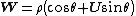 is an elliptic hybrid number, then the roots of
is an elliptic hybrid number, then the roots of 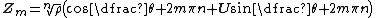
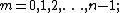
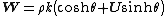 is a spacelike or timelike hyperbolic hybrid number, then the roots of
is a spacelike or timelike hyperbolic hybrid number, then the roots of 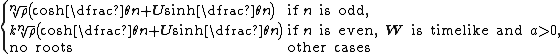
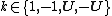 ;
;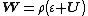 ,
, 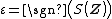 is a parabolic hybrid number, the only root is
is a parabolic hybrid number, the only root is
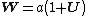 is a lightlike hybrid number, then
is a lightlike hybrid number, then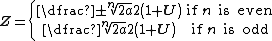
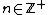 where
where 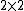 matrix rings
matrix rings 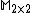 .
. is a ring isomorphism where
is a ring isomorphism where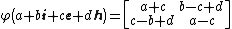
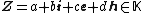 .
.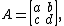
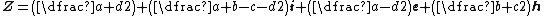
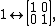
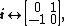
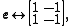
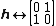
 be a 2 by 2 real matrix corresponding to the hybrid number
be a 2 by 2 real matrix corresponding to the hybrid number 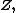 then there are the following equalities.
then there are the following equalities.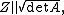
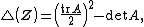
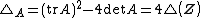 is discriminant of the characteristic polynomial of
is discriminant of the characteristic polynomial of 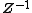 exists if and only if
exists if and only if 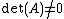 .
.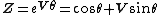
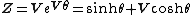
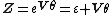 ,
,