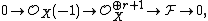“Jouanolou's trick”的意思、由来-开放百科全书

词条

Jouanolou's trick

释义

Jouanolou's construction
Thomason's construction
Bibliography
References

In algebraic geometry, Jouanolou's trick is a theorem that asserts, for an algebraic variety X, the existence of a surjection with affine fibers from an affine variety W to X. The variety W is therefore homotopy-equivalent to X, but it has the technically advantageous property of being affine. Jouanolou's original statement of the theorem required that X be quasi-projective over an affine scheme, but this has since been considerably weakened.

Jouanolou's construction

Jouanolou's original statement was:

If X is a scheme quasi-projective over an affine scheme, then there exists a vector bundle E over X and an affine E-torsor W.

By the definition of a torsor, W comes with a surjective map to X and is Zariski-locally on X an affine space bundle.

Jouanolou's proof used an explicit construction. Let S be an affine scheme and 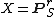. Interpret the affine space 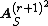as the space of (r + 1) × (r + 1) matrices over S. Within this affine space, there is a subvariety W consisting of idempotent matrices of rank one. The image of such a matrix is therefore a point in X, and the map 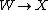that sends a matrix to the point corresponding to its image is the map claimed in the statement of the theorem. To show that this map has the desired properties, Jouanolou notes that there is a short exact sequence of vector bundles:

where the first map is defined by multiplication by a basis of sections of 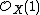and the second map is the cokernel. Jouanolou then asserts that W is a torsor for .

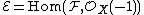Jouanolou deduces the theorem in general by reducing to the above case. If X is projective over an affine scheme S, then it admits a closed immersion into some projective space 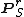. Pulling back the variety W constructed above for 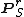along this immersion yields the desired variety W for X. Finally, if X is quasi-projective, then it may be realized as an open subscheme of a projective S-scheme. Blow up the complement of X to get , and let 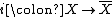denote the inclusion morphism. The complement of X in is a Cartier divisor, and therefore i is an affine morphism. Now perform the previous construction for and pull back along i.

Thomason's construction

Robert Thomason observed that, by making a less explicit construction, it was possible to obtain the same conclusion under significantly weaker hypotheses. Thomason's construction first appeared in a paper of Weibel. Thomason's theorem asserts:

Let X be a quasicompact and quasiseparated scheme with an ample family of line bundles. Then an affine vector bundle torsor over X exists.

Having an ample family of line bundles was first defined in SGA 6 Exposé II Définition 2.2.4. Any quasi-projective scheme over an affine scheme has an ample family of line bundles, as does any separated locally factorial Noetherian scheme.

Thomason's proof abstracts the key features of Jouanolou's. By hypothesis, X admits a set of line bundles L₀, ..., L_N and sections s₀, ..., s_N whose non-vanishing loci are affine and cover X. Define X_i to be the non-vanishing locus of s_i, and define to be the direct sum of L₀, ..., L_N. The sections define a morphism of vector bundles . Define to be the cokernel of s. On X_i, s is a split monomorphism since it is inverted by the inverse of s_i. Therefore is a vector bundle over X_i, and because these open sets cover X, is a vector bundle.

Define 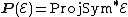and similarly for 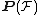. Let W be the complement of 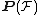in 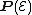. There is an equivalent description of W as 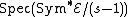, and from this description, it is easy to check that it is a torsor for . Therefore the projection 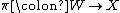is affine. To see that W is itself affine, apply a criterion of Serre (EGA II 5.2.1(b), EGA IV₁ 1.7.17). Each s_i determines a global section f_i of W. The non-vanishing locus W_i of f_i is contained in 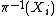, which is affine, and hence W_i is affine. The sum of the sections f₀, ..., f_N is 1, so the ideal they generate is the ring of global sections. Serre's criterion now implies that W is affine.

Bibliography

Jouanolou, Jean-Pierre, Une Suite exact de Mayer–Vietoris en K-Theorie Algebrique. In Algebraic K-theory, I: Higher K-theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), pp. 293–316. Lecture Notes in Math., Vol. 341. Springer, Berlin, 1973.
Weibel, Charles A, Homotopy algebraic K-theory. In Algebraic K-theory and algebraic number theory (Honolulu, HI, 1987), volume 83 of Contemp. Math., pp. 461–488. Amer. Math. Soc., Providence, RI, 1989.

References

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。