回归模型regression model

用数理统计方法建立的描述因变量与自变量之间相关关系的数学模型。变量之间的关系有两类，一类是完全确定的称为函数关系； 另一类是因变量与自变量之间相互关联，但并不完全确定的关系，称为相关关系。电压与电流之间的关系是函数关系； 人的体重与身高、粮食产量与化肥投放量之间的关系是相关关系。
回归分析是数理统计诸方法中应用最广的一种方法。早在19世纪就以最小二乘法的形式在实际中应用。建立回归模型并验证其有效性是回归分析的中心内容。
回归模型的主要作用是： ❶根据一个或几个自变量的值，预测或控制因变量的值，并求出这种预测或控制可达到的精度；
❷因素分析。例如在诸自变量中找出重要的与次要的，并分析它们之间的关系等。
按自变量是一个还是多个，可分为一元回归模型和多元回归模型。按所建模型的性质可分为线性回归模型和非线性回归模型。按建立模型的方法或其他准则，还有多项式回归模型、样条回归模型、逐步回归模型、自回归模型和岭回归模型等。
一元回归模型 只涉及一个自变量和一个因变量的回归模型。是最简单、最基本的回归模型。其一般形式是：

＝a+bx (1)

式中 为因变量数学期望的估计值，a为常数，b为自变量x对因变量y的回归系数。a、b的理论值是难以确定的，只能通过若干次独立试验获得一系列x与y的观察值(x_i,y_i)(i=1,2，…，n,n为试验次数)。每次独立试验所获得的一组x与y的观察值称为一个样本。然后按适当的原则来求a、b的估计值。最常用的是最小二乘法。另外还可用最小方差法和极大似然法。
最小二乘法 根据使因变量的观察值y_i与回归模型的估计值之差的平方和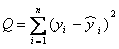最小的原则来估计回归模型参数a、b的一种数理统计方法。由式(1)得到回归模型估计值

Q有极小值，因此可得a、b的估计式：

式中
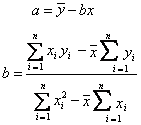
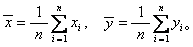
相关系数 表示两个变量线性相关关系程度的数量指标。通常用r表示。

r=0，说明y与x没有线性相关关系。|r|=1，说明所有观察值都符合回归模型，称为y与x完全线性相关。此时y与x存在确定的线性函数关系。r=1为完全正相关，r=-1为完全负相关。0<|r|<1，说明y与x存在一定的线性相关关系，是最常见的情形。r>0,y随x增大而增大，称为y与x正相关；r<0, y随x增大而减小，称为y与x负相关。|r|越大，数据点就越靠近回归直线。
对于给定的样本个数和置信度，利用数理统计的有关知识可以确定一临界相关系数r_min。当r≥min时，则可以认为回归模型以该置信度有效。r_min可从有关的数学用表上查得。
显著性检验 引入假设H₀:b=0。若假设H₀成立，则y与x没有线性相关关系。|b|越大，表明y随x变化的趋势越明显； |b|越小，则趋势越不明显。一元回归模型的显著性检验方法有t检验法和F检验法等。
残差分析 利用实际观察值与回归模型估计值之差对数据的可靠性、周期性或其他干扰进行分析。通过残差分析可以检查是否有异常数据，数据是否有周期性变化，数据是否有倾向性变化及回归模型是否合适等。
预测 用回归模型进行预测时，要根据自变量取值x0，用回归模型求出₀作为预测值。并求其在给定置信水平下的置信区间。只有当x₀落在建立回归模型时的样本值的范围内时，预测才有意义。服从正态分布，它与剩余标准差S有下述关系：落在0±S区间内的可能性为68%；落在y0±2S区间内的可能性为95%；落在₀±3S区间内的可能性为99.7%。因此，可把剩余标准差作为预测精确度的标志。剩余标准差S的计算式为：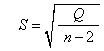

控制 对于因变量y要求的取值范围(y₁,y₂)，求x所应控制的范围。即求相应的x₁,x₂，使x₁2时，x所对应的以要求的置信度落在(y₁,y₂)内。
多元线性回归模型 描述一个因变量与多个自变量间线性相关关系的回归模型。其一般形式为：

＝a+b₁x₁+b₂x₂+…+b_mx_m (2)

式中a为常数；为因变量期望值的估计值；x_j(j=1,2，…，m)为自变量；b_i(i=1,2，…，m)为各自变量的回归系数。
进行n次试验，可得n组观察值(y_i,x_i1,x_i2，…，x_im),i=1,2，…，n(n>m)，它们应有下列关系：

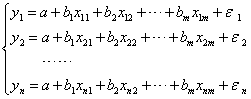
式中 x_ij是第i次试验中第j个自变量的观察值；ε₁,ε₂，…，ε_n是随机误差，它们的均值为零，服从相同的分布，且相互独立。
多元线性回归的显著性检验分为两部分，一是对回归模型的显著性检验。提出假设H₀:b₁＝b₂＝…=b_m＝0，如果H₀被接受，则表明以该模型来表示y与自变量x₁,x₂，…，x_m的相关关系不合适。一般用F检验法。二是对回归系数的显著性检验。提出m个假设H_0i: b_i＝0(i=1,2，…，m)，如H_0i被接受，说明第i个自变量对y的线性作用不显著，应予剔除。常用t检验法。
多元线性回归模型常用逐步回归法来建立，此时称为逐步回归模型。这种方法是从一个自变量开始，按自变量对y作用的显著程度，从大到小依次逐个引入回归模型；并随时对所有变量进行检验，一旦发现由于后面变量的引入而变得不显著的变量，则予以剔除，直到无法引进也无法剔除时即得到最优回归模型。
非线性回归模型 描述因变量与自变量之间非线性相关关系的回归模型。在有些情况下，模型可以通过适当变换化为线性的。例如对于非线性回归模型＝AX^B，两边取对数并以y′, x′分别代换ln、lnx，则可化为下列线性回归模型：

y′=a+bx′

式中 a=1nA,b=B。
对于一般的非线性回归问题，常用下面两种模型进行描述。
多项式回归模型 相当广泛的非线性关系都可用多项式去逼近。其一般形式为：

＝a+ b₁x+b₂x²+…+b_mx^m (3)

多项式次数视情况而定。按多元线性回归模型的方法处理。多项式回归模型的计算量随m的增大而急剧增大。若自变量为等间隔变化时，利用正交多项式可以大大减少计算量。
样条回归模型 把样本的自变量区间分成若干段，各用适当的多项式进行拟合而得的回归模型。也叫分段回归模型。
在自变量的不同范围内，因变量y的变化规律可能并不相同。如果在整个样本自变量区间上建立多项式回归模型，往往需要较高次数的多项式。次数过高的多项式不仅计算量很大，而且振动较大，很不稳定。
自回归模型 参见时间序列模型。