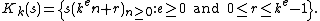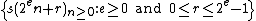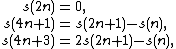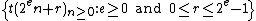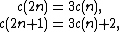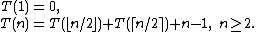- Definition k-kernel Linear combinations Formal series Automata-theoretic
- History
- Examples Ruler sequence Thue–Morse sequence Cantor numbers Sorting numbers Other sequences
- Properties
- Notes
- References
In mathematics and theoretical computer science, a k-regular sequence is a sequence satisfying linear recurrence equations that reflect the base-k representations of the integers. The class of k-regular sequences generalizes the class of k-automatic sequences to alphabets of infinite size.
Definition
There exist several characterizations of k-regular sequences, all of which are equivalent. Some common characterizations are as follows. For each, we take R′ to be a commutative Noetherian ring and we take R to be a ring containing R′.
k-kernel
Let k ≥ 2. The k-kernel of the sequence 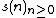 is the set of subsequences
is the set of subsequences
The sequence 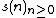 is (R′, k)-regular (often shortened to just "k-regular") if the
is (R′, k)-regular (often shortened to just "k-regular") if the  -module generated by Kk(s) is a finitely-generated R′-module.[1]
-module generated by Kk(s) is a finitely-generated R′-module.[1]
In the special case when 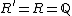 , the sequence
, the sequence 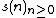 is
is  -regular if
-regular if 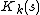 is contained in a finite-dimensional vector space over
is contained in a finite-dimensional vector space over  .
.
Linear combinations
A sequence s(n) is k-regular if there exists an integer E such that, for all ej > E and 0 ≤ rj ≤ kej − 1, every subsequence of s of the form s(kejn + rj) is expressible as an R′-linear combination 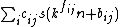 , where cij is an integer, fij ≤ E, and 0 ≤ bij ≤ kfij − 1.[2]
, where cij is an integer, fij ≤ E, and 0 ≤ bij ≤ kfij − 1.[2]
Alternatively, a sequence s(n) is k-regular if there exist an integer r and subsequences s1(n), ..., sr(n) such that, for all 1 ≤ i ≤ r and 0 ≤ a ≤ k − 1, every sequence si(kn + a) in the k-kernel Kk(s) is an R′-linear combination of the subsequences si(n).[2]
Formal series
Let x0, ..., xk − 1 be a set of k non-commuting variables and let τ be a map sending some natural number n to the string xa0 ... xae − 1, where the base-k representation of x is the string ae − 1...a0. Then a sequence s(n) is k-regular if and only if the formal series 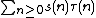 is
is 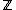 -rational.[3]
-rational.[3]
Automata-theoretic
The formal series definition of a k-regular sequence leads to an automaton characterization similar to Schützenberger's matrix machine.[4][5]
History
The notion of k-regular sequences was first investigated in a pair of papers by Allouche and Shallit.[6] Prior to this, Berstel and Reutenauer studied the theory of rational series, which is closely related to k-regular sequences.[7]
Examples
Ruler sequence
Let 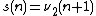 be the
be the  -adic valuation of
-adic valuation of  . The ruler sequence
. The ruler sequence 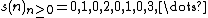 ({{OEIS2C|id=A007814}}) is
({{OEIS2C|id=A007814}}) is  -regular, and the
-regular, and the  -kernel
-kernel
is contained in the two-dimensional vector space generated by 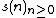 and the constant sequence
and the constant sequence 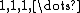 . These basis elements lead to the recurrence relations
. These basis elements lead to the recurrence relations
which, along with the initial conditions 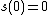 and
and 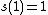 , uniquely determine the sequence.[8]
, uniquely determine the sequence.[8]
Thue–Morse sequence
The Thue–Morse sequence t(n) ({{OEIS2C|id=A010060}}) is the fixed point of the morphism 0 → 01, 1 → 10. It is known that the Thue–Morse sequence is 2-automatic. Thus, it is also 2-regular, and its 2-kernel
consists of the subsequences 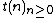 and
and 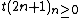 .
.
Cantor numbers
The sequence of Cantor numbers c(n) ({{OEIS2C|id=A005823}}) consists of numbers whose ternary expansions contain no 1s. It is straightforward to show that
and therefore the sequence of Cantor numbers is 2-regular. Similarly the Stanley sequence
0, 1, 3, 4, 9, 10, 12, 13, 27, 28, 30, 31, 36, 37, 39, 40, ... {{OEIS|A005836}}
of numbers whose ternary expansions contain no 2s is also 2-regular.[9]
Sorting numbers
A somewhat interesting application of the notion of k-regularity to the broader study of algorithms is found in the analysis of the merge sort algorithm. Given a list of n values, the number of comparisons made by the merge sort algorithm are the sorting numbers, governed by the recurrence relation
As a result, the sequence defined by the recurrence relation for merge sort, T(n), constitutes a 2-regular sequence.[10]
Other sequences
If  is an integer-valued polynomial, then
is an integer-valued polynomial, then 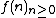 is k-regular for every
is k-regular for every 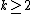 .
.
Allouche and Shallit give a number of additional examples of k-regular sequences in their papers.[6]
Properties
k-regular sequences exhibit a number of interesting properties.
- Every k-automatic sequence is k-regular.[11]
- Every k-synchronized sequence is k-regular.
- A k-regular sequence takes on finitely many values if and only if it is k-automatic.[12] This is an immediate consequence of the class of k-regular sequences being a generalization of the class of k-automatic sequences.
- The class of k-regular sequences is closed under termwise addition, termwise multiplication, and convolution. The class of k-regular sequences is also closed under scaling each term of the sequence by an integer λ.[12][13][14][15]
- For multiplicatively independent k, l ≥ 2, if a sequence is both k-regular and l-regular, then the sequence satisfies a linear recurrence.[16] This is a generalization of a result due to Cobham regarding sequences that are both k-automatic and l-automatic.[17]
- The nth term of a k-regular sequence of integers grows at most polynomially in n.[18]
Notes
2. ^1 Allouche & Shallit (1992), Theorem 2.2
3. ^Allouche & Shallit (1992), Theorem 4.3
4. ^Allouche & Shallit (1992), Theorem 4.4
5. ^{{citation | last = Schützenberger | first = M.-P. | title = On the definition of a family of automata | journal = Information and Control | volume = 4 | issue = 2–3 | year = 1961 | pages = 245–270 | doi=10.1016/S0019-9958(61)80020-X }}.
6. ^1 Allouche & Shallit (1992, 2003)
7. ^{{cite book | last1 = Berstel | first1 = Jean | last2 = Reutenauer | first2 = Christophe | title = Rational Series and Their Languages | volume = 12 | series = EATCS Monographs on Theoretical Computer Science | year = 1988 | isbn = 978-3-642-73237-9 | publisher = Springer-Verlag }}
8. ^Allouche & Shallit (1992), Example 8
9. ^Allouche & Shallit (1992), Examples 3 and 26
10. ^Allouche & Shallit (1992), Example 28
11. ^Allouche & Shallit (1992), Theorem 2.3
12. ^1 Allouche & Shallit (2003) p. 441
13. ^Allouche & Shallit (1992), Theorem 2.5
14. ^Allouche & Shallit (1992), Theorem 3.1
15. ^Allouche & Shallit (2003) p. 445
16. ^{{cite journal | first=J. | last=Bell | title=A generalization of Cobham's theorem for regular sequences| journal=Séminaire Lotharingien de Combinatoire | volume=54A | year=2006 }}
17. ^{{cite journal | first=A. | last=Cobham | title=On the base-dependence of sets of numbers recognizable by finite automata | journal=Math. Systems Theory | volume=3 | issue=2 | year=1969 | pages=186–192 | doi=10.1007/BF01746527 }}
18. ^Allouche & Shallit (1992) Theorem 2.10
References
- {{citation | last1 = Allouche | first1 = Jean-Paul | last2 = Shallit | first2 = Jeffrey | author2-link = Jeffrey Shallit | title = The ring of k-regular sequences | journal = Theoret. Comput. Sci. | volume = 98 | issue = 2 | year = 1992 | pages = 163–197 | doi=10.1016/0304-3975(92)90001-v}}.
- {{citation | last1 = Allouche | first1 = Jean-Paul | last2 = Shallit | first2 = Jeffrey | author2-link = Jeffrey Shallit | title = The ring of k-regular sequences, II | journal = Theoret. Comput. Sci. | volume = 307 | year = 2003 | pages = 3–29 | doi=10.1016/s0304-3975(03)00090-2}}.
- {{cite book | last1 = Allouche | first1 = Jean-Paul | last2 = Shallit | first2 = Jeffrey | author2-link = Jeffrey Shallit | isbn = 978-0-521-82332-6 | publisher = Cambridge University Press | title = Automatic Sequences: Theory, Applications, Generalizations | year = 2003 | zbl=1086.11015 }}
- Vauvise
- Vauxaillon
- Vaux, Allier
- Vaux-Andigny
- Vauxbons
- Vaux Brewery
- Vauxbuin
- Vauxcere
- Vaux-Champagne
- Vauxcéré
- Vaux de Cernay
- Vaux-de-Cernay Abbey
- Vaux de Cernay Abbey
- Vaux de Sernay
- Vaux (disambiguation)
- Vaux-en-Amienois
- Vaux-en-Amiénois
- Vaux-en-Beaujolais
- Vaux-en-Dieulet
- Vaux-en-Pre
- Vaux-en-Pré
- Vaux-en-Vermandois
- Vaux-et-Chantegrue
- Vauxhall 10-4
- Vauxhall 30-98