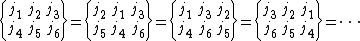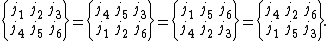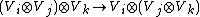- Symmetry relations
- Special case
- Orthogonality relation
- Asymptotics
- Mathematical interpretation
- See also
- Notes
- References
- External links
Wigner's 6-j symbols were introduced by Eugene Paul Wigner in 1940 and published in 1965. They are defined as a sum over products of four Wigner 3-j symbols,
The summation is over all six {{math|mi}} allowed by the selection rules of the 3-j symbols.
They are closely related to the Racah W-coefficients, which are used for recoupling 3 angular momenta, although Wigner 6-j symbols have higher symmetry and therefore provide a more efficient means of storing the recoupling coefficients.[1] Their relationship is given by:
Symmetry relations
The 6-j symbol is invariant under any permutation of the columns:
The 6-j symbol is also invariant if upper and lower arguments
are interchanged in any two columns:
These equations reflect the 24 symmetry operations of the automorphism group that leave the associated tetrahedral Yutsis graph with 6 edges invariant: mirror operations that exchange two vertices and a swap an adjacent pair of edges.
The 6-j symbol
is zero unless j1, j2, and j3 satisfy triangle conditions,
i.e.,
In combination with the symmetry relation for interchanging upper and lower arguments this
shows that triangle conditions must also be satisfied for the triads (j1, j5, j6), (j4, j2, j6), and (j4, j5, j3).
Furthermore, the sum of each of the elements of a triad must be an integer. Therefore, the members of each triad are either all integers or contain one integer and two half-integers.
Special case
When j6 = 0 the expression for the 6-j symbol is:
The triangular delta {{math|{j1 j2 j3}}} is equal to 1 when the triad (j1, j2, j3) satisfies the triangle conditions, and zero otherwise. The symmetry relations can be used to find the expression when another j is equal to zero.
Orthogonality relation
The 6-j symbols satisfy this orthogonality relation:
Asymptotics
A remarkable formula for the asymptotic behavior of the 6-j symbol was first conjectured by Ponzano and Regge[2] and later proven by Roberts.[3] The asymptotic formula applies when all six quantum numbers j1, ..., j6 are taken to be large and associates to the 6-j symbol the geometry of a tetrahedron. If the 6-j symbol is determined by the quantum numbers j1, ..., j6 the associated tetrahedron has edge lengths Ji = ji+1/2 (i=1,...,6) and the asymptotic formula is given by,
The notation is as follows: Each θi is the external dihedral angle about the edge Ji of the associated tetrahedron and the amplitude factor is expressed in terms of the volume, V, of this tetrahedron.
Mathematical interpretation
In representation theory, 6-j symbols are matrix coefficients of the associator isomorphism in a tensor category.[4] For example, if we are given three representations Vi, Vj, Vk of a group (or quantum group), one has a natural isomorphism
of tensor product representations, induced by coassociativity of the corresponding bialgebra. One of the axioms defining a monoidal category is that associators satisfy a pentagon identity, which is equivalent to the Biedenharn-Elliot identity for 6-j symbols.
When a monoidal category is semisimple, we can restrict our attention to irreducible objects, and define multiplicity spaces
so that tensor products are decomposed as:
where the sum is over all isomorphism classes of irreducible objects. Then:
The associativity isomorphism induces a vector space isomorphism
and the 6j symbols are defined as the component maps:
When the multiplicity spaces have canonical basis elements and dimension at most one (as in the case of SU(2) in the traditional setting), these component maps can be interpreted as numbers, and the 6-j symbols become ordinary matrix coefficients.
In abstract terms, the 6-j symbols are precisely the information that is lost when passing from a monoidal category to its Grothendieck group, since one can reconstruct a monoidal structure using the associator. For the case of representations of a finite group, the character table, together with its 6-j symbols, uniquely determines the group up to isomorphism, while the character table alone does not.
See also
- Clebsch–Gordan coefficients
- 3-j symbol
- Racah W-coefficient
- 9-j symbol
Notes
2. ^{{cite journal|last=Ponzano G and Regge T|title=Semiclassical Limit of Racah Coefficients|year=1968|pages=1–58|publisher=Amsterdam|location=in Spectroscopy and Group Theoretical Methods in Physics}}
3. ^{{cite journal|last=Roberts J|title=Classical 6j-symbols and the tetrahedron|year=1998|journal=Geometry and Topology|pages=21–66|volume=3|doi=10.2140/gt.1999.3.21|arxiv=math-ph/9812013}}
4. ^{{cite book |last=Etingof |first=P. |author2=Gelaki S.|author3=Nikshych D.|author4=Ostrik V. |title=Tensor Categories |url=http://www-math.mit.edu/~etingof/tenscat1.pdf |year=2009 }}
References
- {{cite book |last1= Biedenharn |first1= L. C. |authorlink=Lawrence Biedenharn |last2= van Dam |first2=H.
|title= Quantum Theory of Angular Momentum: A collection of Reprints and Original Papers
|year= 1965 |publisher= Academic Press |location= New York |isbn= 0-12-096056-7}}
- {{cite book |last= Edmonds |first= A. R. |title= Angular Momentum in Quantum Mechanics |year= 1957
|publisher= Princeton University Press |location= Princeton, New Jersey |isbn= 0-691-07912-9}}
- {{cite book |last= Condon |first= Edward U. |author2= Shortley, G. H. |title= The Theory of Atomic Spectra |year= 1970
|publisher= Cambridge University Press |location= Cambridge |isbn= 0-521-09209-4 |chapter= Chapter 3}}
- {{dlmf|id=34 |title=3j,6j,9j Symbols|first=Leonard C.|last= Maximon}}
- {{cite book |last= Messiah |first= Albert |authorlink=Albert Messiah |title= Quantum Mechanics (Volume II) |year= 1981 | edition= 12th
|publisher= North Holland Publishing |location= New York |isbn= 0-7204-0045-7}}
- {{cite book |last= Brink |first= D. M. |author2= Satchler, G. R. |title= Angular Momentum
|year= 1993 |edition= 3rd |publisher= Clarendon Press |location= Oxford |isbn= 0-19-851759-9 |chapter= Chapter 2 }}
- {{cite book |last= Zare |first= Richard N. |title= Angular Momentum |year=1988
|publisher= John Wiley |location= New York |isbn= 0-471-85892-7 |chapter= Chapter 2}}
- {{cite book |last= Biedenharn |first= L. C. |author2= Louck, J. D. |title= Angular Momentum in Quantum Physics
|year= 1981 |publisher= Addison-Wesley |location= Reading, Massachusetts |isbn= 0-201-13507-8 }}
External links
- {{cite journal
|journal=Nuovo Cimento
|first1=T.
|last1=Regge
|title=Simmetry Properties of Racah's Coefficients
|volume=11
|issue=1
|year=1959
|doi=10.1007/BF02724914
|pages=116–117
|bibcode=1959NCim...11..116R
}}
- {{cite web
|first1=Anthony
|last1=Stone
|url=http://www-stone.ch.cam.ac.uk/wigner.shtml
|title=Wigner coefficient calculator
}} (Gives exact answer)
- {{cite web |url=http://geoweb.princeton.edu/people/simons/software.html |first1=Frederik J.|last1=Simons|title=Matlab software archive, the code SIXJ.M}}
- {{cite web
|first1 = A
|last1 = Volya
|url = http://www.volya.net/vc
|archive-url = https://archive.is/20121220081850/http://www.volya.net/vc
|dead-url = yes
|archive-date = 2012-12-20
|title = Clebsch-Gordan, 3-j and 6-j Coefficient Web Calculator
}}
- {{cite web
|url=http://plasma-gate.weizmann.ac.il/369j.html
|title=369j-symbol calculator
|author=Plasma Laboratory of Weizmann Institute of Science
}}
- {{ cite web
|url=https://www.gnu.org/software/gsl/manual/html_node/Coupling-Coefficients.html
|title=Coupling coefficients
|author=GNU scientific library
}}
- {{cite web
|first1=Richard J.
|last1=Mathar
|title=(Python implementation)
|url=https://arxiv.org/src/1102.5125v2/anc
}} [https://arxiv.org/src/0908.3030v2/anc Java implementation]
- {{cite web
|first1=H.T.
|last1=Johansson
|first2=C.
|last2=Forssén
|title=(WIGXJPF)
|url=http://fy.chalmers.se/subatom/wigxjpf/
}} (accurate; C, fortran, python)
- {{cite web
|first1=H.T.
|last1=Johansson
|title=(FASTWIGXJ)
|url=http://fy.chalmers.se/subatom/fastwigxj/
}} (fast lookup, accurate; C, fortran)
- European Tennis Association
- European Tenpin Bowling Federation
- European theater of operations
- European Theater of Operations Ribbon
- European theater of World War II
- European theatre of world war i
- European theatre of World War I
- European theatre of world war ii
- European Theatre of WWII
- European Theological Seminary and College of the Bible International
- European theological seminary and college of the bible international
- European Tire and Rim Technical Organisation
- European Tire and Rim Technical Organization
- European Top 100 Albums
- European Top 20
- European tort law
- European Touring Car Championship
- European tournament
- European tournaments
- European Tour rookie of the year
- European Tour Rookie of the Year
- European Tour's
- European trademark law
- European trade mark law
- European Trademark Office