- Formulation
- Solution
- Algorithms Exact Solution of Exponential Complexity Exact Solution of Polynomial Complexity Approximate Efficient Solvers L1-BF Algorithm
- Complex Data
- Code
- References
L1-PCA is often preferred over standard L2-norm principal component analysis (PCA) when the analyzed data may contain outliers (faulty values or corruptions).[2][3][4]
Both L1-PCA and standard PCA seek a collection of orthogonal directions (principal components) that define a subspace wherein data representation is maximized according to the selected criterion.[5][6][7]
Standard PCA quantifies data representation as the aggregate of the L2-norm of the data point projections into the subspace, or equivalently the aggregate Euclidean distance of the original points from their subspace-projected representations.
L1-PCA uses instead the aggregate of the L1-norm of the data point projections into the subspace.[8] In PCA and L1-PCA, the number of principal components (PCs) is lower than the rank of the analyzed matrix, which coincides with the dimensionality of the space defined by the original data points.
Therefore, PCA or L1-PCA are commonly employed for dimensionality reduction for the purpose of data denoising or compression.
Among the advantages of standard PCA that contributed to its high popularity are low-cost computational implementation by means of singular-value decomposition (SVD)[9] and statistical optimality when the data set is generated by a true multivariate Normal data source.
However, in modern big data sets, data often include corrupted, faulty points, commonly referred to as outliers.[10]
Standard PCA is known to be sensitive to outliers, even when they appear as a small fraction of the processed data.[11]
The reason is that the L2-norm formulation of L2-PCA places squared emphasis on the magnitude of each coordinate of each data point, ultimately overemphasizing peripheral points, such as outliers.
On the other hand, following an L1-norm formulation, L1-PCA places linear emphasis on the coordinates of each data point, effectively restraining outliers.[12]
Formulation
Consider any matrix 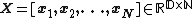 consisting of
consisting of 
 -dimensional data points. Define
-dimensional data points. Define 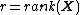 . For integer
. For integer  such that
such that 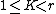 , L1-PCA is formulated as:[1]
, L1-PCA is formulated as:[1]
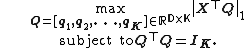
|{{EquationRef|1}}}}
For 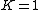 , ({{EquationNote|1}}) simplifies to finding the L1-norm principal component (L1-PC) of
, ({{EquationNote|1}}) simplifies to finding the L1-norm principal component (L1-PC) of  by
by
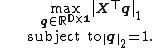
|{{EquationRef|2}}}}
In ({{EquationNote|1}})-({{EquationNote|2}}), L1-norm 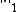 returns the sum of the absolute entries of its argument and L2-norm
returns the sum of the absolute entries of its argument and L2-norm 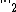 returns the sum of the squared entries of its argument. If one substitutes
returns the sum of the squared entries of its argument. If one substitutes 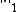 in ({{EquationNote|2}}) by the Frobenius/L2-norm
in ({{EquationNote|2}}) by the Frobenius/L2-norm  , then the problem becomes standard PCA and it is solved by the matrix
, then the problem becomes standard PCA and it is solved by the matrix  that contains the
that contains the  dominant singular vectors of
dominant singular vectors of  (i.e., the singular vectors that correspond to the
(i.e., the singular vectors that correspond to the  highest singular values).
highest singular values).
The maximization metric in ({{EquationNote|2}}) can be expanded as
{{NumBlk|:|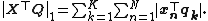
|{{EquationRef|3}}}}
Solution
For any matrix 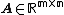 with
with 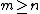 , define
, define 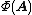 as the nearest (in the L2-norm sense) matrix to
as the nearest (in the L2-norm sense) matrix to 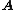 that has orthonormal columns. That is, define
that has orthonormal columns. That is, define

|{{EquationRef|4}}}}
Procrustes Theorem[13][14] states that if 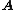 has SVD
has SVD 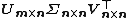 , then
, then
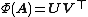 .
.
Markopoulos, Karystinos, and Pados[1] showed that, if 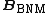 is the exact solution to the binary nuclear-norm maximization (BNM) problem
is the exact solution to the binary nuclear-norm maximization (BNM) problem
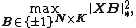
|{{EquationRef|5}}}}
then
{{NumBlk|:|
|{{EquationRef|6}}}}
is the exact solution to L1-PCA in ({{EquationNote|2}}). The nuclear-norm 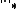 in ({{EquationNote|2}}) returns the summation of the singular values of its matrix argument and can be calculated by means of standard SVD. Moreover, it holds that, given the solution to L1-PCA,
in ({{EquationNote|2}}) returns the summation of the singular values of its matrix argument and can be calculated by means of standard SVD. Moreover, it holds that, given the solution to L1-PCA, 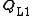 , the solution to BNM can be obtained as
, the solution to BNM can be obtained as
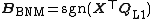
|{{EquationRef|7}}}}
where 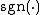 returns the
returns the 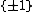 -sign matrix of its matrix argument (with no loss of generality, we can consider
-sign matrix of its matrix argument (with no loss of generality, we can consider 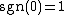 ). In addition, it follows that
). In addition, it follows that 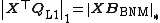 . BNM in ({{EquationNote|5}}) is a combinatorial problem over antipodal binary variables. Therefore, its exact solution can be found through exhaustive evaluation of all
. BNM in ({{EquationNote|5}}) is a combinatorial problem over antipodal binary variables. Therefore, its exact solution can be found through exhaustive evaluation of all 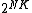 elements of its feasibility set, with asymptotic cost
elements of its feasibility set, with asymptotic cost 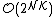 . Therefore, L1-PCA can also be solved, through BNM, with cost
. Therefore, L1-PCA can also be solved, through BNM, with cost 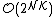 (exponential in the product of the number of data points with the number of the sought-after components). It turns out that L1-PCA can be solved optimally (exactly) with polynomial complexity in
(exponential in the product of the number of data points with the number of the sought-after components). It turns out that L1-PCA can be solved optimally (exactly) with polynomial complexity in  for fixed data dimension
for fixed data dimension  ,
, 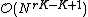 .[1]
.[1]
For the special case of 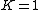 (single L1-PC of
(single L1-PC of  ), BNM takes the binary-quadratic-maximization (BQM) form
), BNM takes the binary-quadratic-maximization (BQM) form
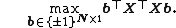
|{{EquationRef|8}}}}
The transition from ({{EquationNote|5}}) to ({{EquationNote|8}}) for 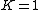 holds true, since the unique singular value of
holds true, since the unique singular value of 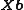 is equal to
is equal to  , for every
, for every 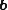 . Then, if
. Then, if 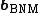 is the solution to BQM in ({{EquationNote|7}}), it holds that
is the solution to BQM in ({{EquationNote|7}}), it holds that
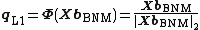
|{{EquationRef|9}}}}
is the exact L1-PC of  , as defined in ({{EquationNote|1}}). In addition, it holds that
, as defined in ({{EquationNote|1}}). In addition, it holds that  and
and 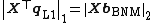 .
.
Algorithms
Exact Solution of Exponential Complexity
As shown above, the exact solution to L1-PCA can be obtained by the following two-step process:
1. Solve the problem in ({{EquationNote|5}}) to obtain 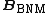 . 2. Apply SVD on
. 2. Apply SVD on 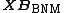 to obtain
to obtain 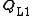 .
.BNM in ({{EquationNote|5}}) can be solved by exhaustive search over the domain of 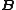 with cost
with cost 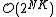 .
.
Exact Solution of Polynomial Complexity
Also, L1-PCA can be solved optimally with cost 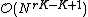 , when
, when 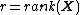 is constant with respect to
is constant with respect to  (always true for finite data dimension
(always true for finite data dimension  ).[1][15]
).[1][15]
Approximate Efficient Solvers
In 2008, Kwak[12] proposed an iterative algorithm for the approximate solution of L1-PCA for 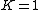 . This iterative method was later generalized for
. This iterative method was later generalized for 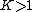 components.[16] Another approximate efficient solver was proposed by McCoy and Tropp[17] by means of semi-definite programming (SDP). Most recently, L1-PCA (and BNM in ({{EquationNote|5}})) were solved efficiently by means of bit-flipping iterations (L1-BF algorithm).[8][24]
components.[16] Another approximate efficient solver was proposed by McCoy and Tropp[17] by means of semi-definite programming (SDP). Most recently, L1-PCA (and BNM in ({{EquationNote|5}})) were solved efficiently by means of bit-flipping iterations (L1-BF algorithm).[8][24]
L1-BF Algorithm
1 '''function''' L1BF(,
): 2 Initialize
and
3 Set
and
4 Until termination (or
iterations) 5
,
6 For
7
,
8
''// flip bit'' 9
''// calculated by SVD or faster (see[8])'' 10 if
11
,
12
13 end 14 if
''// no bit was flipped'' 15 if
16 terminate 17 else 18
The computational cost of L1-BF is 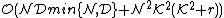 .[8]
.[8]
Complex Data
L1-PCA has also been generalized to process complex data. For complex L1-PCA, two efficient algorithms were proposed in 2018.[18]
Code
MATLAB code for L1-PCA is available at MathWorks[19] and other repositories.[20]References
2. ^{{cite journal|last1=Barrodale|first1=I.|title=L1 Approximation and the Analysis of Data|journal=Applied Statistics|date=1968|volume=17|issue=1|pages=51–57|doi=10.2307/2985267|jstor=2985267}}
3. ^{{cite book|last1=Barnett|first1=Vic|last2=Lewis|first2=Toby|title=Outliers in statistical data|date=1994|publisher=Wiley|location=Chichester [u.a.]|isbn=978-0471930945|edition=3.}}
4. ^{{cite book|last1=Kanade|first1=T.|last2=Ke|first2=Qifa|title=Robust L1 Norm Factorization in the Presence of Outliers and Missing Data by Alternative Convex Programming|journal=2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05)|volume=1|pages=739|date=June 2005|doi=10.1109/CVPR.2005.309|publisher=IEEE|isbn=978-0-7695-2372-9|citeseerx=10.1.1.63.4605}}
5. ^{{cite book|last1=Jolliffe|first1=I.T.|title=Principal component analysis|date=2004|publisher=Springer|location=New York|isbn=978-0387954424|edition=2nd}}
6. ^{{cite book|last1=Bishop|first1=Christopher M.|title=Pattern recognition and machine learning|date=2007|publisher=Springer|location=New York|isbn=978-0-387-31073-2|edition=Corr. printing.}}
7. ^{{cite journal|last1=Pearson|first1=Karl|title=On Lines and Planes of Closest Fit to Systems of Points in Space|journal=The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science|date=8 June 2010|volume=2|issue=11|pages=559–572|doi=10.1080/14786440109462720}}
8. ^1 2 3 {{cite journal|last1=Markopoulos|first1=Panos P.|last2=Kundu|first2=Sandipan|last3=Chamadia|first3=Shubham|last4=Pados|first4=Dimitris A.|title=Efficient L1-Norm Principal-Component Analysis via Bit Flipping|journal=IEEE Transactions on Signal Processing|date=15 August 2017|volume=65|issue=16|pages=4252–4264|doi=10.1109/TSP.2017.2708023|arxiv=1610.01959|bibcode=2017ITSP...65.4252M}}
9. ^{{cite journal|last1=Golub|first1=Gene H.|title=Some Modified Matrix Eigenvalue Problems|journal=SIAM Review|date=April 1973|volume=15|issue=2|pages=318–334|doi=10.1137/1015032|citeseerx=10.1.1.454.9868}}
10. ^{{cite book|last1=Barnett|first1=Vic|last2=Lewis|first2=Toby|title=Outliers in statistical data|date=1994|publisher=Wiley|location=Chichester [u.a.]|isbn=978-0471930945|edition=3.}}
11. ^{{cite journal|last1=Candès|first1=Emmanuel J.|last2=Li|first2=Xiaodong|last3=Ma|first3=Yi|last4=Wright|first4=John|title=Robust principal component analysis?|journal=Journal of the ACM|date=1 May 2011|volume=58|issue=3|pages=1–37|doi=10.1145/1970392.1970395|arxiv=0912.3599}}
12. ^1 {{cite journal|last1=Kwak|first1=N.|title=Principal Component Analysis Based on L1-Norm Maximization|journal=IEEE Transactions on Pattern Analysis and Machine Intelligence|date=September 2008|volume=30|issue=9|pages=1672–1680|doi=10.1109/TPAMI.2008.114|pmid=18617723|citeseerx=10.1.1.333.1176}}
13. ^{{cite journal|last1=Eldén|first1=Lars|last2=Park|first2=Haesun|title=A Procrustes problem on the Stiefel manifold|journal=Numerische Mathematik|date=1 June 1999|volume=82|issue=4|pages=599–619|doi=10.1007/s002110050432|citeseerx=10.1.1.54.3580}}
14. ^{{cite journal|last1=Schönemann|first1=Peter H.|title=A generalized solution of the orthogonal procrustes problem|journal=Psychometrika|date=March 1966|volume=31|issue=1|pages=1–10|doi=10.1007/BF02289451}}
15. ^{{cite book|last1=Markopoulos|first1=PP|last2=Kundu|first2=S|last3=Chamadia|first3=S|last4=Tsagkarakis|first4=N|last5=Pados|first5=DA|title=Outlier-Resistant Data Processing with L1-Norm Principal Component Analysis|journal=Advances in Principal Component Analysis|date=2018|issue=Springer, Singapore|pages=121|doi=10.1007/978-981-10-6704-4_6|isbn=978-981-10-6703-7}}
16. ^{{cite journal|last1=Nie|first1=F|last2=Huang|first2=H|last3=Ding|first3=C|last4=Luo|first4=Dijun|last5=Wang|first5=H|title=Robust principal component analysis with non-greedy l1-norm maximization|journal=22nd International Joint Conference on Artificial Intelligence|date=July 2011|pages=1433–1438}}
17. ^{{cite journal|last1=McCoy|first1=Michael|last2=Tropp|first2=Joel A.|date=2011|title=Two proposals for robust PCA using semidefinite programming|journal=Electronic Journal of Statistics|volume=5|pages=1123–1160|doi=10.1214/11-EJS636}}
18. ^{{cite journal|last1=Tsagkarakis|first1=Nicholas|last2=Markopoulos|first2=Panos P.|last3=Sklivanitis|first3=George|last4=Pados|first4=Dimitris A.|title=L1-Norm Principal-Component Analysis of Complex Data|journal=IEEE Transactions on Signal Processing|date=15 June 2018|volume=66|issue=12|pages=3256–3267|doi=10.1109/TSP.2018.2821641|arxiv=1708.01249|bibcode=2018ITSP...66.3256T}}
19. ^{{cite web|title=L1-PCA TOOLBOX|url=https://www.mathworks.com/matlabcentral/fileexchange/64855-l1-pca-toolbox|accessdate=May 21, 2018}}
20. ^1 {{cite web|last1=Markopoulos|first1=PP|url=https://people.rit.edu/pxmeee/soft.html|title=Software Repository|accessdate=May 21, 2018}}
- Wicked Bronze Ambition
- Wicked Chief
- Wicked City (1949 film)
- Wicked City (film)
- Wicked City (Hideyuki Kikuchi novel)
- Wicked City (TV series)
- Wicked Cyclone (Six Flags New England)
- Wickede (Dortmund)
- Wicked Evolution
- Wicked Fairy Godmother
- Wicked Game (album)
- Wicked Game (disambiguation)
- Wicked Game (Gemma Hayes)
- Wicked Game (Gemma Hayes song)
- Wicked Game (Il Divo album)
- Wicked Games
- Wicked Game (singel)
- Wicked Game (single)
- Wicked Grin
- Wicked is good
- Wicked Is the Vine
- Wickedleak wammy passion x
- Wickedleak Wammy Passion X
- Wicked little high
- Wicked Local