“Lawvere–Tierney topology”的意思、由来-开放百科全书

词条

Lawvere–Tierney topology

释义

Definition
j-closure
Examples
References

In mathematics, a Lawvere–Tierney topology is an analog of a Grothendieck topology for an arbitrary topos, used to construct a topos of sheaves. A Lawvere–Tierney topology is also sometimes also called a local operator or coverage or topology or geometric modality. They were introduced by {{harvs|txt|authorlink=William Lawvere|last=Lawvere|first=William|year=1971}} and Myles Tierney.

Definition

If E is a topos, then a topology on E is a morphism j from the subobject classifier Ω to Ω such that j preserves truth (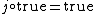), preserves intersections (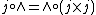), and is idempotent ().

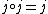j-closure

Given a subobject 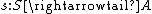of an object A with classifier 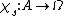, then the composition 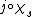defines another subobject 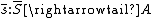of A such that s is a subobject of 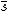, and 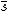is said to be the j-closure of s.

Some theorems related to j-closure are (for some subobjects s and w of A):

inflationary property:
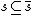
idempotence:
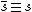
preservation of intersections:
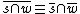
preservation of order:
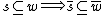
stability under pullback: .

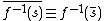Examples

Grothendieck topologies on a small category C are essentially the same as Lawvere–Tierney topologies on the topos of presheaves of sets over C.

References

{{citation|mr=0430021

|last=Lawvere|first= F. W.|authorlink=William Lawvere
|chapter=Quantifiers and sheaves|title= Actes du Congrès International des Mathématiciens (Nice, 1970)|volume= 1|pages= 329–334|publisher= Gauthier-Villars|place= Paris|year= 1971|url=https://pdfs.semanticscholar.org/6630/846a00261a071b71e264e0f532e29cd9152f.pdf}}

{{citation|last1=Mac Lane|first1=Saunders|author1-link=Saunders Mac Lane|last2=Moerdijk|first2=Ieke|author2-link=Ieke Moerdijk|year=1994|title=Sheaves in geometry and logic. A first introduction to topos theory|series=Universitext|publisher=Springer-Verlag|location=New York}}. Corrected reprint of the 1992 edition.
{{citation|last=McLarty|first=Colin|authorlink=Colin McLarty|title=Elementary Categories, Elementary Toposes|series=Oxford Logic Guides|publisher=Oxford University Press|location=New York|page=196|year=1995|origyear=1992}}

2 : Topos theory|Closure operators

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。