- Definition à la Ginzburg–Kapranov
- Notes
- References
- External links
In mathematics, the Lie operad is an operad whose algebras are Lie algebras. The notion (at least one version) was introduced by {{harvtxt|Ginzburg|Kapranov|1994}} in their formulation of Koszul duality.
Definition à la Ginzburg–Kapranov
Let 
denote the free Lie algebra (over some field) with the generators 
and 
the subspace spanned by all the bracket monomials containing each 
exactly once. The symmetric group 
acts on by permutations and, under that action,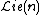 
is invariant. Hence, 
is an operad.[1]
The Koszul-dual of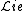 
is the commutative-ring operad, an operad whose algebras are commutative rings.
Notes
1. ^{{harvnb|Ginzburg|Kapranov|1994||loc=§ 1.3.9.}}
References
- {{citation
| last1 = Ginzburg | first1 = Victor
| last2 = Kapranov | first2 = Mikhail
| doi = 10.1215/S0012-7094-94-07608-4
| issue = 1
| journal = Duke Mathematical Journal
| mr = 1301191
| pages = 203–272
| title = Koszul duality for operads
| volume = 76
| year = 1994}}
External links
- Todd Trimble, Notes on operads and the Lie operad
- https://ncatlab.org/nlab/show/Lie+operad
1 : Algebra
- Monkey's Eyebrow
- Monkeys Eyebrow, KY
- Monkey's fist knot
- Monkeys, Go Home!
- Monkey shakspeare simulator
- Monkey's head mushroom
- Monkeyshines, No. 1
- Monkeyshines, No. 2
- Monkeyshines, No. 3
- Monkeys in ships
- Monkeys in Winter
- Monkey's paw knot
- Monkey Spunk
- Monkeys typewriters
- Monkeys typing Hamlet
- Monkeys typing Shakespeare
- Monkey Temple
- Monkey temple
- Monkey Thieves
- Monkey Thieves (TV series)
- Monkey Thieves (TV Show)
- Monkey to Man
- Monkey tree
- Monkey Turn
- Monkey typewriters