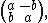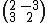“Matrix field”的意思、由来-开放百科全书

词条

Matrix field

释义

Examples
See also
References

In abstract algebra, a matrix field is a field with matrices as elements. In field theory we come across two type of fields: finite field and infinite field. There are several examples of matrix fields of finite and infinite order. In general, corresponding to each field of numbers there is a matrix field.

There is a finite matrix field of order p for each positive prime p.^[1] One can find several finite matrix field of order p for any given positive prime p. In general, corresponding to each finite field there is a matrix field. However any two finite fields of equal order are algebraically equivalent. The elements of a finite field can be represented by matrices.^[2] In this way one can construct a finite matrix field.

Contrary to the general case for matrix multiplication, multiplication is commutative in a matrix field (if the usual operations are used). Since addition and multiplication of matrices have all needed properties for field operations except for commutativity of multiplication, one way to verify if a set of matrices is a field with the usual operations of matrix sum and multiplication is to check whether

the neutral elements for sum and multiplication (that is, the zero matrix and the identity matrix) are included;
the set is closed under addition and multiplication; and
multiplication is commutative.

However, it may be possible to construct fields of matrices using other operations -- in which case it would be necessary to verify all properties of the operations in the set in order to guarantee that it is a field.

Examples

1. The set of all diagonal matrices of order n over the field of rational (real or complex) numbers is a matrix field of infinite order under addition and multiplication of matrices.

2. The set of all diagonal matrices of order two over the field of integers modulo p (a positive prime) forms a finite matrix field of order p under addition and multiplication of matrices modulo p.

3. (a negative example) It does not suffice for multiplication to commute in order to obtain a field of matrices. Take the set of all matrices of the form

with -- that is, matrices filled with zeroes except for the -th row, which is filled with the same real constant .

These matrices are commutative for multiplication:

However, there is no neutral element for multiplication, since this needs to be the identity matrix, and it is not included in the set, so this is not a matrix field.

4. The set of all matrices of order two of the form

over the real numbers (or over any other field), with the usual operations of matrix sum and matrix multiplication.

The zero matrix (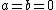) and the identity matrix (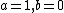) are included. Summing two of these matrices results in another matrix of the same form:

The same is true for multiplication:

Finally, multiplication is commutative for these matrices:

5. As a particular case of example 4, taking and ranging over the reals, one obtains the field of matrices of the form

which is isomorphic to the field 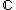of the complex numbers: corresponds to the real part of the number, while correspods to the imaginary part. So the number , for example, would be represented as

One can easily verify, for example, that :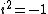

and also, by computing a matrix exponential, that Euler's identity, is also valid:

6. As another particular case of example 4, a field of matrices

with square-free and rationals is isomorphic to the quadratic field .

References

1. ^{{cite journal|last1=Pandey|first1=S. K.|title=Matrix Field of Finite and Infinite Order|journal=International Research Journal of Pure Algebra|volume=5|issue=12|pages=214–216 | year=2015 |}}
2. ^{{cite book| | last=Lidl | first=Rudolf | last2=Niederreiter | first2=Harald | author2-link = Harald Niederreiter | title=Introduction to finite fields and their applications| edition=1st | year=1986 | publisher=Cambridge University Press | isbn=0-521-30706-6 }}

3 : Field theory|Algebraic structures|Matrices

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Examples

See also

References