请输入您要查询的百科知识：

　

词条 Minimum relevant variables in linear system
释义

  1. Definition

  2. Special case

  3. Applications

  4. Related problems

  5. Hardness of approximation

  6. References

MINimum Relevant Variables in Linear System (Min-RVLS) is a problem in mathematical optimization. Given a linear program, it is required to find a feasible solution in which the number of non-zero variables is as small as possible.

The problem is known to be NP-hard and even hard to approximate.

Definition

A Min-RVLS problem is defined by:[1]

  • A binary relation R, which is one of {=, ≥, >, ≠};
  • An m-by-n matrix A (where m is the number of constraints and n the number of variables);
  • An m-by-1 vector b.

The linear system is given by: A x R b. It is assumed to be feasible (i.e., satisfied by at least one x). Depending on R, there are four different variants of this system: A x = b, A x ≥ b, A x > b, A x ≠ b.

The goal is to find an n-by-1 vector x that satisfies the system A x R b, and subject to that, contains as few as possible nonzero elements.

Special case

The problem Min-RVLS[=] was presented by Garey and Johnson,[2] who called it "minimum weight solution to linear equations". They proved it was NP-hard, but did not consider approximations.

Applications

The Min-RVLS problem is important in machine learning and linear discriminant analysis. Given a set of positive and negative examples, it is required to minimize the number of features that are required to correctly classify them.[3] The problem is known as the minimum feature set problem. An algorithm that approximates Min-RVLS within a factor of 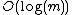could substantially reduce the number of training samples required to attain a given accuracy level. [4]

The shortest codeword problem in coding theory is the same problem as Min-RVLS[=] when the coefficients are in GF(2).

Related problems

In MINimum Unsatisfied Linear Relations (Min-ULR), we are given a binary relation R and a linear system A x R b, which is now assumed to be infeasible. The goal is to find a vector x that violates as few relations as possible, while satisfying all the others.

Min-ULR[≠] is trivially solvable, since any system with real variables and a finite number of inequality constraints is feasible. As for the other three variants:

  • Min-ULR[=,>,≥] are NP-hard even with homogeneous systems and bipolar coefficients (coefficients in {1,-1}). [5]
  • The NP-complete problem Minimum feedback arc set reduces to Min-ULR[≥], with exactly one 1 and one -1 in each constraint, and all right-hand sides equal to 1. [6]
  • Min-ULR[=,>,≥] are polynomial if the number of variables n is constant: they can be solved polynomially using an algorithm of Greer[7] in time .
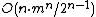  • Min-ULR[=,>,≥] are linear if the number of constraints m is constant, since all subsystems can be checked in time O(n).
  • Min-ULR[≥] is polynomial in some special case.[6]
  • Min-ULR[=,>,≥] can be approximated within n + 1 in polynomial time.[1]
  • Min-ULR[>,≥] are minimum-dominating-set-hard, even with homogeneous systems and ternary coefficients (in {−1,0,1}).
  • Min-ULR[=] cannot be approximated within a factor of 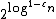, for any , unless NP is contained in DTIME(). [8]

In the complementary problem MAXimum Feasible Linear Subystem (Max-FLS), the goal is to find a maximum subset of the constraints that can be satisfied simultaneously.[5]

  • Max-FLS[≠] can be solved in polynomial time.
  • Max-FLS[=] is NP-hard even with homogeneous systems and bipolar coefficients.
  • . With integer coefficients, it is hard to approximate within . With coefficients over GF[q], it is q-approximable.
  • Max-FLS[>] and Max-FLS[≥] are NP-hard even with homogeneous systems and bipolar coefficients. They are 2-approximable, but they cannot be approximated within any smaller constant factor.

Hardness of approximation

All four variants of Min-RVLS are hard to approximate. In particular all four variants cannot be approximated within a factor of 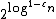, for any , unless NP is contained in DTIME().[1]{{Rp|247-250}} The hardness is proved by reductions:

  • There is a reduction from Min-ULR[=] to Min-RVLS[=]. It also applies to Min-RVLS[≥] and Min-RVLS[>], since each equation can be replaced by two complementary inequalities.
  • There is a reduction from minimum-dominating-set to Min-RVLS[≠].

On the other hand, there is a reduction fro Min-RVLS[=] to Min-ULR[=]. It also applies to Min-ULR[≥] and Min-ULR[>], since each equation can be replaced by two complementary inequalities.

Therefore, when R is in {=,>,≥}, Min-ULR and Min-RVLS are equivalent in terms of approximation hardness.

References

1. ^1 2 {{Cite journal|date=1998-12-06|title=On the approximability of minimizing nonzero variables or unsatisfied relations in linear systems|journal=Theoretical Computer Science|language=en|volume=209|issue=1–2|pages=237–260|doi=10.1016/S0304-3975(97)00115-1|issn=0304-3975|last1=Amaldi|first1=Edoardo|last2=Kann|first2=Viggo}}
2. ^{{Cite web|url=https://www.semanticscholar.org/paper/Computers-and-Intractability:-A-Guide-to-the-Theory-Garey-Johnson/1e3b61f29e5317ef59d367e1a53ba407912d240e|title=Computers and Intractability: A Guide to the Theory of NP-Completeness|last=Johnson|first=David S.|last2=Garey|first2=M. R.|date=1979|website=www.semanticscholar.org|language=en|access-date=2019-01-07}}
3. ^{{Cite journal|last=Koehler|first=Gary J.|date=1991-11-01|title=Linear Discriminant Functions Determined by Genetic Search|journal=ORSA Journal on Computing|volume=3|issue=4|pages=345–357|doi=10.1287/ijoc.3.4.345|issn=0899-1499}}
4. ^{{Cite journal|last=Van Horn|first=Kevin S.|last2=Martinez|first2=Tony R.|date=1994-03-01|title=The Minimum Feature Set Problem|journal=Neural Netw.|volume=7|issue=3|pages=491–494|doi=10.1016/0893-6080(94)90082-5|issn=0893-6080}}
5. ^1 {{Cite journal|date=1995-08-07|title=The complexity and approximability of finding maximum feasible subsystems of linear relations|url=https://www.sciencedirect.com/science/article/pii/030439759400254G|journal=Theoretical Computer Science|language=en|volume=147|issue=1–2|pages=181–210|doi=10.1016/0304-3975(94)00254-G|issn=0304-3975|last1=Amaldi|first1=Edoardo|last2=Kann|first2=Viggo}}
6. ^1 {{Cite journal|date=1993-02-01|title=A note on resolving infeasibility in linear programs by constraint relaxation|url=https://www.sciencedirect.com/science/article/pii/016763779390079V|journal=Operations Research Letters|language=en|volume=13|issue=1|pages=19–20|doi=10.1016/0167-6377(93)90079-V|issn=0167-6377|last1=Sankaran|first1=Jayaram K.}}
7. ^{{Cite book|url=https://books.google.com/?id=DRxEqwzbb2UC&pg=PP1&dq=Trees+and+hills:+Methodology+for+maximizing+functions+of+systems+of+linear+relations,#v=onepage&q=Trees%20and%20hills:%20Methodology%20for%20maximizing%20functions%20of%20systems%20of%20linear%20relations,&f=false|title=Trees and Hills: Methodology for Maximizing Functions of Systems of Linear Relations|last=Greer|first=R.|date=2011-08-18|publisher=Elsevier|isbn=9780080872070|language=en}}
8. ^{{Cite journal|date=1997-04-01|title=The Hardness of Approximate Optima in Lattices, Codes, and Systems of Linear Equations|journal=Journal of Computer and System Sciences|language=en|volume=54|issue=2|pages=317–331|doi=10.1006/jcss.1997.1472|issn=0022-0000|last1=Arora|first1=Sanjeev|last2=Babai|first2=László|last3=Stern|first3=Jacques|last4=Sweedyk|first4=Z.}}

4 : Linear programming|NP-hard problems|Approximation algorithms|Combinatorial optimization
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/9/22 8:33:36