图tu

用平面上的点以及两点间的联线构成的，且只涉及点线位置关系，而与线的长短无关的几何图形.
例如，一般交通图，只需画出以点表示的地名及两点联线表示的二地之间的交通线(仅当需要知道运费或距离时，才在交通线旁标上数字).又如，若干人集会，可用点表示人，两点间有联线表示二人相识等等.
一般，G=〈V,E〉，称为图，其中V={v₁,v₂，…，v_n},vi称为点(顶点、结点),V称为G的点集；E={e₁,e₂，…，e_m},ei称为边，E称为G的边集.每个e_i联接着V的一对点v_j,v_k后，记成e_i＝v_jv_k.
当e_i＝v_jv_k,v_jv_k称为e_i的端点，称e_i关联于v_jv_k；称v_j,v_k是邻接的（点）.
当e=v_iv_i，即e的二端点是同一个点，则e称为v的自回路（或环），若二点间的边不只一条，这种边称为（多）重边或平行边.若边e₁,e₂有一公共端点，则称e₁,e₂是邻接的（边）.
没有环也没有重边的图称为简单图.有重边或环的图称为伪图.
若边e是有方向的称为有向边.用以表示如单行线方向，领导关系，比赛中的胜负等；否则称为无向边.若图G的所有边都是有向边，称为有向图，如图可表示一场比赛，v_iv_j表示v_i胜；G的边均无方向，称为无向图.若G的一些边有方向而另一些边无方向，则称为混合图.若图G的每条边e都联系一个实数w(e)，则G称为赋权图（或带权图），如标了票价或距离的交通图.

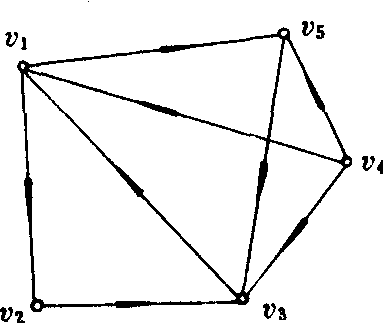
用图的方法可以证明，在n(n≥2)个人中，总有（至少）两个人在该人群中有相同的朋友数.用n个点表示这n个人，当且仅当两人是朋友时，代表他们的点间有联线。注意到每人或没有朋友或至多有n-1个朋友.并且当有人没有朋友时，则余下的人中不可能有人有n-1个朋友.于是，所有n个点的度数(参见“点的度数”)或在0,1,2，…，n-2中出现，或在1,2，…，n-1中出现.于是，至少有2点，它们的度数相同，即该二人有相同的朋友数.
若图G=〈V,E〉的一部分点及一部分边构成图G₁，即G₁＝〈V₁,E₁〉，V₁⊆V,E₁⊆E，则G₁称为G之子图.当G₁＝〈V,E₁〉，E₁⊆E，则G₁称为G的生成子图.
如下图，G₁和G₂皆为G的两个生成子图.

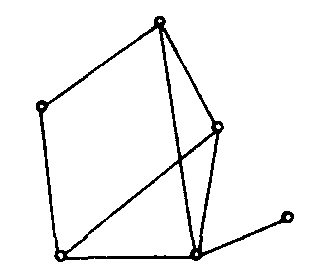
G

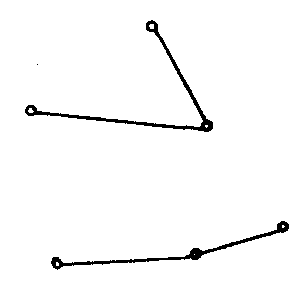
G₁

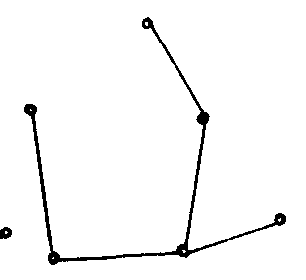
G₂