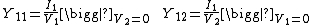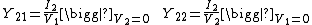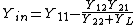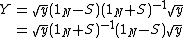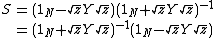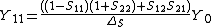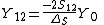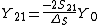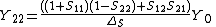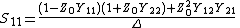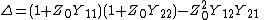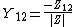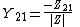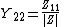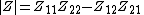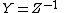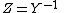- The Y-parameter matrix
- Two-port networks Admittance relations
- Relation to S-parameters Two port
- Relation to Z-parameters
- Notes
- References
- See also
The Y-parameter matrix
A Y-parameter matrix describes the behaviour of any linear electrical network that can be regarded as a black box with a number of ports. A port in this context is a pair of electrical terminals carrying equal and opposite currents into and out of the network, and having a particular voltage between them. The Y-matrix gives no information about the behaviour of the network when the currents at any port are not balanced in this way (should this be possible), nor does it give any information about the voltage between terminals not belonging to the same port. Typically, it is intended that each external connection to the network is between the terminals of just one port, so that these limitations are appropriate.
For a generic multi-port network definition, it is assumed that each of the ports is allocated an integer n ranging from 1 to N, where N is the total number of ports. For port n, the associated Y-parameter definition is in terms of the port voltage and port current,  and
and 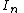 respectively.
respectively.
For all ports the currents may be defined in terms of the Y-parameter matrix and the voltages by the following matrix equation:
where Y is an N × N matrix the elements of which can be indexed using conventional matrix notation. In general the elements of the Y-parameter matrix are complex numbers and functions of frequency. For a one-port network, the Y-matrix reduces to a single element, being the ordinary admittance measured between the two terminals.
Two-port networks
The Y-parameter matrix for the two-port network is probably the most common. In this case the relationship between the port voltages, port currents and the Y-parameter matrix is given by:
.
where
For the general case of an N-port network,
Admittance relations
The input admittance of a two-port network is given by:
where YL is the admittance of the load connected to port two.
Similarly, the output admittance is given by:
where YS is the admittance of the source connected to port one.
Relation to S-parameters
The Y-parameters of a network are related to its S-Parameters by[5]
and[5]
where 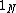 is the identity matrix,
is the identity matrix,  is a diagonal matrix having the square root of the characteristic admittance (the reciprocal of the characteristic impedance) at each port as its non-zero elements,
is a diagonal matrix having the square root of the characteristic admittance (the reciprocal of the characteristic impedance) at each port as its non-zero elements,
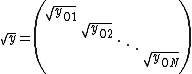
and  is the corresponding diagonal matrix of square roots of characteristic impedances. In these expressions the matrices represented by the bracketed factors commute and so, as shown above, may be written in either order.[5][6]
is the corresponding diagonal matrix of square roots of characteristic impedances. In these expressions the matrices represented by the bracketed factors commute and so, as shown above, may be written in either order.[5][6]
Two port
In the special case of a two-port network, with the same and real characteristic admittance  at each port, the above expressions reduce to [7]
at each port, the above expressions reduce to [7]
Where
The above expressions will generally use complex numbers for  and
and 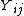 . Note that the value of
. Note that the value of  can become 0 for specific values of
can become 0 for specific values of  so the division by
so the division by  in the calculations of
in the calculations of 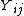 may lead to a division by 0.
may lead to a division by 0.
The two-port S-parameters may also be obtained from the equivalent two-port Y-parameters by means of the following expressions.[8]
where
and 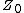 is the characteristic impedance at each port (assumed the same for the two ports).
is the characteristic impedance at each port (assumed the same for the two ports).
Relation to Z-parameters
Conversion from Z-parameters to Y-parameters is much simpler, as the Y-parameter matrix is just the inverse of the Z-parameter matrix. The following expressions show the applicable relations:
Where
In this case 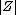 is the determinant of the Z-parameter matrix.
is the determinant of the Z-parameter matrix.
Vice versa the Y-parameters can be used to determine the Z-parameters, essentially using the
same expressions since
And
Notes
2. ^Pozar, David M. (2005) (op. cit); pp 170-174.
3. ^Pozar, David M. (2005) (op. cit); pp 183-186.
4. ^Morton, A. H. (1985); Advanced Electrical Engineering;Pitman Publishing Ltd.; pp 33-72. {{ISBN|0-273-40172-6}}
5. ^1 2 {{cite book |title=Electromagnetics, microwave circuit and antenna design for communications engineering |last=Russer |first=Peter |year=2003 |publisher=Artech House |isbn=978-1-58053-532-8}}
6. ^Any square matrix commutes with itself and with the identity matrix, and if two matrices A and B commute, then so do A and B−1 (since AB−1 = B−1BAB−1 = B−1ABB−1 = B−1A)
7. ^{{Cite journal|last=Frickey|first=D. A.|date=February 1994|title=Conversions between S, Z, Y, H, ABCD, and T parameters which are valid for complex source and load impedances|url=http://ieeexplore.ieee.org/document/275248/|journal=IEEE Transactions on Microwave Theory and Techniques|volume=42|issue=2|pages=205–211|doi=10.1109/22.275248|issn=0018-9480}}
8. ^Simon Ramo, John R. Whinnery, Theodore Van Duzer, "Fields and Waves in Communication Electronics", Third Edition, John Wiley & Sons Inc.; 1993, pp. 537-541, {{ISBN|0-471-58551-3}}.
References
See also
- Nodal admittance matrix
- Scattering parameters
- Impedance parameters
- Two-port network
- Hybrid-pi model
- Power gain
- Edough massif
- Edourad Filliol
- Edourd Burdzhalov
- Ed Owen
- Edo Wonderland Nikko Edomura
- Ed Oxenbould
- Edoya
- Edoy Church
- Edoyfjorden
- Edo Šen
- Edpa
- Ed Parry
- Ed Pasquale
- EDP audit
- EDP Brasil
- EDP Cernavoda Wind Farm
- Ed Pearlman
- Ed Peirce
- Ed Peletier
- EDP - Energias de Portugal
- EDP-Energias de Portugal
- EDP-Energias do Brasil
- EDP Energias do Brasil
- Edper
- Edper Enterprises