- Problem formulation
- Solution concepts
- Solution methods
- Related problem classes
- References
Multi-objective linear programming is a subarea of mathematical optimization. A multiple objective linear program (MOLP) is a linear program with more than one objective function. An MOLP is a special case of a vector linear program. Multi-objection linear programming is also a subarea of Multi-objective optimization.
Problem formulation
In mathematical terms, a MOLP can be written as:
where  is an
is an 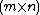 matrix,
matrix,  is a
is a 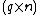 matrix,
matrix,  is an
is an  -dimensional vector with components in
-dimensional vector with components in 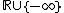 ,
,  is an
is an  -dimensional vector with components in
-dimensional vector with components in 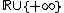 ,
,  is an
is an  -dimensional vector with components in
-dimensional vector with components in 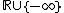 ,
,  is an
is an  -dimensional vector with components in
-dimensional vector with components in 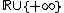
Solution concepts
A feasible point  is called efficient if there is no feasible point
is called efficient if there is no feasible point  with
with 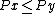 ,
, 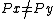 , where
, where  denotes the component-wise ordering.
denotes the component-wise ordering.
Often in the literature, the aim in multiple objective linear programming is to compute the set of all efficient extremal points....[1]. There are also algorithms to determine the set of all maximal efficient faces [2]. Based on these goals, the set of all efficient (extreme) points can seen to be the solution of MOLP. This type of solution concept is called decision set based[3]. It is not compatible with an optimal solution of a linear program but rather parallels the set of all optimal solutions of a linear program (which is more difficult to determine).
Efficient points are frequently called efficient solutions. This term is misleading because a single efficient point can be already obtained by solving one linear program, such as the linear program with the same feasible set and the objective function being the sum of the objectives of MOLP[4].
More recent references consider outcome set based solution concepts[5] and corresponding algorithms[6][3]. Assume MOLP is bounded, i.e. there is some 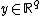 such that
such that 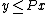 for all feasible
for all feasible  . A solution of MOLP is defined to be a finite subset
. A solution of MOLP is defined to be a finite subset 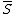 of efficient points that carries a sufficient amount of information in order to describe the upper image of MOLP. Denoting by
of efficient points that carries a sufficient amount of information in order to describe the upper image of MOLP. Denoting by  the feasible set of MOLP, the upper image of MOLP is the set
the feasible set of MOLP, the upper image of MOLP is the set 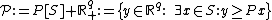 . A formal definition of a solution [5][7] is as follows:
. A formal definition of a solution [5][7] is as follows:
A finite set 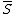 of efficient points is called solution to MOLP if
of efficient points is called solution to MOLP if
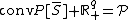 ("conv" denotes the convex hull).
("conv" denotes the convex hull).
If MOLP is not bounded, a solution consists not only of points but of points and directions [7][11]
Solution methods
Multiobjective variants of the simplex algorithm are used to compute decision set based solutions[1][2][8] and objective set based solutions.[9]
Objective set based solutions can be obtained by Benson's algorithm.[3][10]
Related problem classes
Multiobjective linear programming is equivalent to polyhedral projection.[11]
References
2. ^1 {{cite journal|last1=Ecker|first1=J. G.|last2=Hegner|first2=N. S.|last3=Kouada|first3=I. A.|title=Generating all maximal efficient faces for multiple objective linear programs|journal=Journal of Optimization Theory and Applications|volume=30|issue=3|year=1980|pages=353–381|issn=0022-3239|doi=10.1007/BF00935493}}
3. ^1 2 {{cite journal|title=An outer approximation algorithm for generating all efficient extreme points in the outcome set of a multiple objective linear programming problem|last1=Benson|first1=Harold P.|journal=Journal of Global Optimization|volume=13|issue=1|year=1998|pages=1–24|issn=09255001|doi=10.1023/A:1008215702611}}
4. ^{{cite book|last1=Ehrgott|first1=M.|title=Multicriteria Optimization|journal=Springer|year=2005|doi=10.1007/3-540-27659-9|isbn=978-3-540-21398-7|citeseerx=10.1.1.360.5223}}
5. ^1 {{cite journal|last1=Heyde|first1=Frank|last2=Löhne|first2=Andreas|title=Solution concepts in vector optimization: a fresh look at an old story|journal=Optimization|volume=60|issue=12|year=2011|pages=1421–1440|issn=0233-1934|doi=10.1080/02331931003665108}}
6. ^{{cite journal|last1=Dauer|first1=J.P.|last2=Saleh|first2=O.A.|title=Constructing the set of efficient objective values in multiple objective linear programs|journal=European Journal of Operational Research|volume=46|issue=3|year=1990|pages=358–365|issn=03772217|doi=10.1016/0377-2217(90)90011-Y}}
7. ^1 {{cite book|title=Vector Optimization with Infimum and Supremum|last1=Löhne|first1=Andreas|year=2011|issn=1867-8971|doi=10.1007/978-3-642-18351-5|series=Vector Optimization|isbn=978-3-642-18350-8}}
8. ^{{cite journal|last1=Armand|first1=P.|last2=Malivert|first2=C.|title=Determination of the efficient set in multiobjective linear programming|journal=Journal of Optimization Theory and Applications|volume=70|issue=3|year=1991|pages=467–489|issn=0022-3239|doi=10.1007/BF00941298|citeseerx=10.1.1.161.9730}}
9. ^{{cite journal|last1=Rudloff|first1=Birgit|last2=Ulus|first2=Firdevs|last3=Vanderbei|first3=Robert|title=A parametric simplex algorithm for linear vector optimization problems|journal=Mathematical Programming|volume=163|issue=1–2|year=2016|pages=213–242|issn=0025-5610|doi=10.1007/s10107-016-1061-z|arxiv=1507.01895}}
10. ^1 {{cite journal|last1=Löhne|first1=Andreas|last2=Weißing|first2=Benjamin|title=The vector linear program solver Bensolve – notes on theoretical background|journal=European Journal of Operational Research|volume=260|issue=3|year=2017|pages=807–813|issn=03772217|doi=10.1016/j.ejor.2016.02.039|arxiv=1510.04823}}
11. ^{{cite journal|last1=Löhne|first1=Andreas|last2=Weißing|first2=Benjamin|title=Equivalence between polyhedral projection, multiple objective linear programming and vector linear programming|journal=Mathematical Methods of Operations Research|volume=84|issue=2|year=2016|pages=411–426|issn=1432-2994|doi=10.1007/s00186-016-0554-0|arxiv=1507.00228}}
- Hamilton Daily Democrat
- Hamilton Daily News
- Hamilton Daily Sun
- Hamilton-Dalrymple Baronets
- Hamilton de Holanda
- Hamilton Democrat-Sun
- Hamilton de Oliveira
- Hamilton Disston School
- Hamilton Distillers
- Hamilton District Christian High School
- Hamilton Division
- Hamilton East electorate
- Hamilton East School
- Hamilton East—Stoney Creek (provincial electoral district)
- Hamilton E. James
- Hamilton, Elizabeth
- Hamiltonella
- Hamiltonella defensa
- Hamilton-Ely Farmstead
- Hamilton Emilio Cuvi
- Hamilton Evening Journal
- Hamilton Everhart Farm
- Hamilton Eye Institute
- Hamilton Family Estate
- Hamilton Farm Petroglyphs