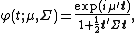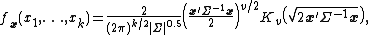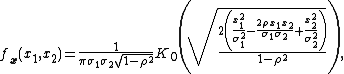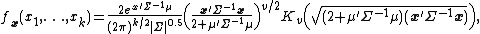“Multivariate Laplace distribution”的意思、由来-开放百科全书

词条

Multivariate Laplace distribution

释义

Symmetric multivariate Laplace distribution
Probability density function
Asymmetric multivariate Laplace distribution
References

{{Probability distribution
| name = Multivariate Laplace (symmetric)
| type = multivariate
| pdf_image =
| cdf_image =
| notation =
| parameters = μ ∈ R^k — location
Σ ∈ R^k×k — covariance (positive-definite matrix)
| support = x ∈ μ + span(Σ) ⊆ R^k
| pdf = :

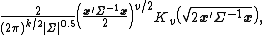
where

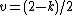and

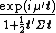{{Probability distribution
| name = Multivariate Laplace (asymmetric)
| type = multivariate
| pdf_image =
| cdf_image =
| notation =
| parameters = μ ∈ R^k — location
Σ ∈ R^k×k — covariance (positive-definite matrix)
| support = x ∈ μ + span(Σ) ⊆ R^k
| pdf =

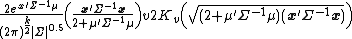
where

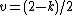and

In the mathematical theory of probability, multivariate Laplace distributions are extensions of the Laplace distribution and the asymmetric Laplace distribution to multiple variables. The marginal distributions of symmetric multivariate Laplace distribution variables are Laplace distributions. The marginal distributions of asymmetric multivariate Laplace distribution variables are asymmetric Laplace distributions.^[1]

Symmetric multivariate Laplace distribution

A typical characterization of the symmetric multivariate Laplace distribution has the characteristic function:

where 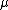is the vector of means for each variable and 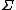is the covariance matrix.^[2]

Unlike the multivariate normal distribution, even if the covariance matrix has zero covariance and correlation the variables are not independent.^[1] The symmetric multivariate Laplace distribution is elliptical.^[1]

Probability density function

If 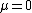, the probability density function (pdf) for a k-dimensional multivariate Laplace distribution becomes:

where:

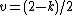and

is the modified Bessel function of the second kind.^[1]

In the correlated bivariate case, i.e., k = 2, with 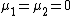the pdf reduces to:

where:

and

are the standard deviations of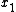

and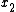

, respectively, and

is the correlation coefficient of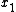

and

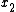.^[1]

For the independent bivariate Laplace case, that is k = 2, 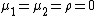and 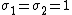, the pdf becomes:

^[1]

Asymmetric multivariate Laplace distribution

A typical characterization of the asymmetric multivariate Laplace distribution has the characteristic function:

^[1]

As with the symmetric multivariate Laplace distribution, the asymmetric multivariate Laplace distribution has mean 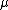, but the covariance becomes 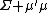.^[3] The asymmetric multivariate Laplace distribution is not elliptical unless 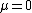, in which case the distribution reduces to the symmetric multivariate Laplace distribution with 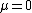.^[1]

The probability density function (pdf) for a k-dimensional asymmetric multivariate Laplace distribution is:

where:

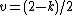and

is the modified Bessel function of the second kind.^[1]

The asymmetric Laplace distribution, including the special case of 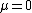, is an example of a geometric stable distribution.^[3] It represents the limiting distribution for a sum of independent, identically distributed random variables with finite variance and covariance where the number of elements to be summed is itself an independent random variable distributed according to a geometric distribution.^[1] Such geometric sums can arise in practical applications within biology, economics and insurance.^[1] The distribution may also be applicable in broader situations to model multivariate data with heavier tails than a normal distribution but finite moments.^[1]

The relationship between the exponential distribution and the Laplace distribution allows for a simple method for simulating bivariate asymmetric Laplace variables (including for the case of 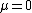). Simulate a bivariate normal random variable vector 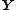from a distribution with 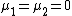and covariance matrix 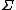. Independently simulate an exponential random variables W from an Exp(1) distribution. 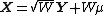will be distributed (asymmetric) bivariate Laplace with mean 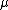and covariance matrix 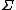.^[1]

References

1. ^¹²³⁴⁵⁶⁷⁸⁹¹⁰¹¹¹²{{cite book|title=The Laplace Distribution and Generalizations|author=Kotz. Samuel; Kozubowski, Tomasz J. & Podgorski, Krzysztof|pages=229–245|year=2001|publisher=Birkhauser|isbn=0817641661}}
2. ^{{cite journal|title=Goodness-of-fit tests for multivariate Laplace distributions|author=Fragiadakis, Konstantinos & Meintanis, Simos G.|url=http://www.sciencedirect.com/science/article/pii/S0895717710004760|accessdate=2017-05-28|journal=Mathematical and Computer Modelling|volume=53|issue=5-6|date=March 2011|pages=769–779|doi=10.1016/j.mcm.2010.10.014}}
3. ^¹{{cite web|title=Multivariate Generalize Laplace Distributions and Related Random Fields|author= Kozubowski, Tomasz J.; Podgorski, Krzysztof & Rychlik, Igor|url=https://pdfs.semanticscholar.org/7c5b/7fc2d0756ad5a161922a9b439e12ccfb51eb.pdf|publisher=University of Gothenburg|accessdate=2017-05-28|year=2010}}

3 : Probability distributions|Multivariate continuous distributions|Geometric stable distributions

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。