请输入您要查询的百科知识：

　

词条 Numerical modeling (geology)
释义

  1. History

  2. Components

  3. Properties

  4. Computation

      Kinematic descriptions    Eulerian    Lagrangian    Governing equations    Continuity equation    Momentum equation   Heat equation    Numerical methods    Finite element method    Spectral method    Finite volume method    Finite difference method    Discrete element method    Bonded-particle model  

  5. Applications

      Specimen to outcrop scale    Rock mechanics    Regional-scale    Thermochronology    Pecube    Hydrogeology    MODFLOW    Crustal dynamics    FLAC    Global-scale    Mantle convection    Finite difference approach    Finite volume approach    Finite element approach    Spectral method    Plate tectonics    Geodynamo    Seismology  

  6. Errors and limitations

      Sources of error    Limitations  

  7. See also

  8. References

In geology, numerical modeling is a widely applied technique to tackle complex geological problems by computational simulation of geological scenarios.

Numerical modeling uses mathematical models to describe the physical conditions of geological scenarios using numbers and equations.[2] Nevertheless, some of their equations are difficult to solve directly, such as partial differential equations. With numerical models, geologists can use methods, such as finite difference methods, to approximate the solutions of these equations. Numerical experiments can then be performed in these models, yielding the results that can be interpreted in the context of geological process.[2] Both qualitative and quantitative understanding of a variety of geological processes can be developed via these experiments.[4]

Numerical modelling has been used to assist in the study of rock mechanics, thermal history of rocks, movements of tectonic plates and the Earth's mantle. Flow of fluids is simulated using numerical methods, and this shows how ground water moves, or how motions of the molten outer core yields the geomagnetic field.

History

Prior to the development of numerical modeling, analog modeling, which simulates nature with reduced scales in mass, length, and time, was one of the major ways to tackle geological problems,[3][4] for instance, to model the formation of thrust belts.[5] Simple analytic or semi-analytic mathematical models were also used to deal with relatively simple geological problems quantitatively.[2]

In the late 1960s to 1970s, following the development of finite-element methods in solving continuum mechanics problems for civil engineering, numerical methods were adapted for modeling complex geological phenomena,[4][6] for example, folding[7][8] and mantle convection.[9] With advances in computer technology, the accuracy of numerical models has been improved.[2] Numerical modeling has become an important tool for tackling geological problems,[2] especially for the parts of the Earth that are difficult to observe directly, such as the mantle and core. Yet analog modeling is still useful in modeling geological scenarios that are difficult to capture in numerical models, and the combination of analog and numerical modeling can be useful to improve understanding of the Earth's processes.[10]

Components

A general numerical model study usually consists of the following components:[11][2]

  1. Mathematical model is a simplified description of the geological problem, such as equations and boundary conditions.&91;2&93; These governing equations of the model are often partial differential equations that are difficult to solve directly since it involves the derivative of the function,&91;12&93; for example, the wave equation.&91;2&93;
  2. Discretization methods and numerical methods convert those governing equations in the mathematical models to discrete equations.&91;2&93; These discrete equations can approximate the solution of the governing equations.&91;2&93; Common methods include the finite element, finite difference, or finite volume method that subdivide the object of interest into smaller pieces (element) by mesh. These discrete equations can then be solved in each element numerically.&91;2&93; The discrete element method uses another approach, this method reassembling the object of interest from numerous tiny particles. Simple governing equations are then applied to the interactions between particles.
  3. Algorithms are computer programs that compute the solution using the idea of the above numerical methods.&91;2&93;
  4. Interpretations are made from the solutions given by the numerical models.&91;2&93;

Properties

A good numerical model usually has some of the following properties:[11][2]

  • Consistent: Numerical models often divide the object into smaller elements. If the model is consistent, the result of the numerical model is nearly the same as what the mathematical model predicts when the element size is nearly zero. In other words, the error between the discrete equations used in the numerical model and the governing equations in the mathematical model tends to zero when the space of the mesh (size of element) becomes close to zero.[2]
  • Stable: In a stable numerical model, the error during the computation of the numerical methods does not amplify.[2] The error of an unstable model will stack up quickly and lead to an incorrect result. A stable and consistent numerical model has the same output as the exact solution in the mathematical model when the spacing of the mesh (size of element) is extremely small.[2]
  • Converging: The output of the numerical model is closer to the actual solution of the governing equations in the mathematical models when the spacing of mesh (size of element) reduces, which is usually checked by carrying out numerical experiments.[2]
  • Conserved: The physical quantities in the models, such as mass and momentum, are conserved.[2] Since the equations in the mathematical models are usually derived from various conservation laws, the model result should not violate these premises.[2]
  • Bounded: The solution given by the numerical model has reasonable physical bounds with respect to the mathematical models, for instance mass and volume should be positive.[2]
  • Accurate: The solution given by the numerical models is close to the real solution predicted by the mathematical model.[2]

Computation

The following are some key aspects of ideas in developing numerical models in geology. First, the way to describe the object and motion should be decided (kinematic description). Then, governing equations that describe the geological problems are written, for example, the heat equations describe the flow of heat in a system. Since some of these equations cannot be solved directly, numerical methods are used to approximate the solution of the governing equations.

Kinematic descriptions

{{Main|Lagrangian and Eulerian specification of the flow field}}

In numerical models and mathematical models, there are two different approaches to describe the motion of matter: Eulerian and Lagrangian.[13] In geology, both approaches are commonly used to model fluid flow like mantle convection, where an Eulerian grid is used for computation and Lagrangian markers are used to visualize the motion.[2] Recently, there have been models that try to describe different parts using different approaches to combine the advantages of these two approaches. This combined approach is called the arbitrary Lagrangian-Eulerian approach.[14]

Eulerian

The Eulerian approach considers the changes of the physical quantities, such as mass and velocity, of a fixed location with time.[13] It is similar to looking at how river water flows past a bridge. Mathematically, the physical quantities can be expressed as a function of location and time. This approach is useful for fluid and homogeneous (uniform) materials that have no natural boundary.[15]

Lagrangian

The Lagrangian approach, on the other hand, considers the change of physical quantities, such as the volume, of fixed elements of matter over time.[13] It is similar to looking at a certain collection of water molecules as they flow downstream in a river. Using the Lagrangian approach, it is easier to follow solid objects which have natural boundary to separate them from the surrounding.[15]

{{Gallery|title=Kinematic descriptions
|align=center|height=320|width=480|File:Eulerian approach to describe motion.gif
|alt1=Eulerian approach
|Eulerian approach In the figure, the orange box indicates the area of interest. In the Eulerian approach, the location of the red box is fixed, while the change of color of that box illustrates the changing value at that position.
|File:Lagrangian approach to describe motion.gif
|alt2=Lagrangian approach
|Lagrangian approach. In the figure, the orange box indicates the area of interest. In the Lagrangian approach, the location of the red box is not fixed, it moves over time. The area of interest is always the same element.
}}

Governing equations

{{Main|Governing equation}}

Following are some basic equations that are commonly used to describe physical phenomena, for example, how the matter in a geologic system moves or flows and how heat energy is distributed in a system. These equations are usually the core of the mathematical model.

Continuity equation

The continuity equation is a mathematical version of stating that the geologic object or medium is continuous, which means no empty space can be found in the object.[16] This equation is commonly used in numerical modeling in geology.[16]

One example is the continuity equation of mass of fluid. Based on the law of conservation of mass, for a fluid with density at position in a fixed volume of fluid, the rate of change of mass is equal to the outward fluid flow across the boundary :

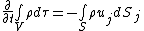
where is the volume element and is the velocity at .

In Lagrangian form:[2]

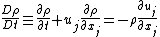
In Eulerian form:[2]

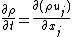
This equation is useful when the model involves continuous fluid flow, like the mantle is over geological time scales.[2]

Momentum equation

{{Main|Equations of motion|Navier–Stokes equations}}The momentum equation describes how matter moves in response to force applied. It is an expression of Newton's second law of motion.[16]

Consider a fixed volume of matter. By the law of conservation of momentum, the rate of change of volume is equal to:[2]

  • external force applied on the element
  • plus normal stress and shear stress applied on the surface bounding the element
  • minus the momentum moving out of the element on that surface

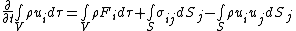
where is the volume element, is the velocity.

After simplifications and integrations, for any volume , the Eulerian form of this equation is:[2][16]

Heat equation

{{Main|Heat equation|Convection–diffusion equation}}The heat equations describe how heat energy flows in a system.

From the law of conservation of energy, the rate of change of energy of a fixed volume of mass is equal to:[2]

  • work done at the boundary
  • plus work done by external force in the volume
  • minus heat conduction across boundary
  • minus heat convection across boundary
  • plus heat produced internally

Mathematically:

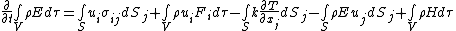
where is the volume element, is the velocity, 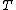is the temperature, is the conduction coefficient and is the rate of heat production.[2]

Numerical methods

Numerical methods are techniques to approximate the governing equations in the mathematical models.

Common numerical methods include finite element method, spectral method, finite difference method, and finite volume method. These methods are used to approximate the solution of governing differential equations in the mathematical model by dissecting the domain into meshes or grids and applying simpler equations to individual elements or nodes in the mesh.[2][17]

The discrete element method uses another approach. The object is considered an assemblage of small particles.[57]

Finite element method

The finite element method subdivides the object (or domain) into smaller, non-overlapping elements (or subdomains) and these elements are connected at the nodes. The solution for the partial differential equations are then approximated by simpler element equations, usually polynomials.[2][18][19] Then these element equations are combined into equations for the entire object, i.e. the contribution of each element is summed up to model the response of the whole object.[2][18][19] This method is commonly used to solve mechanical problems.[19] The following are the general steps of using the finite element method:[19]

  1. Select the element type and subdivide the object. Common element types include triangular, quadrilateral, tetrahedral, etc.&91;19&93; Different types of elements should be chosen for different problems.
  2. Decide the function of displacement. The function of displacement governs how the elements move. Linear, quadratic, or cubic polynomial functions are commonly used.&91;19&93;
  3. Decide the displacement-strain relation. The displacement of the element changes or deforms the element's shape in what is technically called strain. This relation calculates how much strain the element experienced due to the displacement.&91;19&93;
  4. Decide the strain-stress relation. The deformation of the element induces stress to the element, which is the force applied to the element. This relation calculates the amount of stress experienced by the element due to the strain. One of the examples of this relation is Hooke's law.&91;19&93;
  5. Derive equations of stiffness and stiffness matrix for elements. The stress also causes the element to deform; the stiffness (the rigidity) of the elements indicates how much it will deform in response to the stress. The stiffness of the elements in different directions is represented in matrix form for simpler operation during calculation.&91;19&93;
  6. Combine the element equations into global equations. The contributions of every element are summed up to a set of equations that describe the whole system.&91;19&93;
  7. Apply boundary conditions. The predefined conditions at the boundary, such as temperature, stress, and other physical quantities are introduced to the boundary of the system.&91;19&93;
  8. Solve for displacement. As time evolves, the displacement of the elements are solved step by step.&91;19&93;
  9. Solve for strains and stress. After the displacement is calculated, the strains and stress are computed using the relations in steps 3 and 4.&91;19&93;

Spectral method

The spectral method is similar to the finite element method.[75][76] The major difference is that spectral method uses basis functions, possibly by using a Fast Fourier Transformation (FFT) that approximates the function by the sum of numerous simple functions.[75][76] These kinds of basis functions can then be applied to the whole domain and approximate the governing partial differential equations.[2][20][76] Therefore, each calculation takes the information from the whole domain into account while the finite element method only takes the information from the neighborhood.[20][21] As a result, the spectral method converges exponentially and is suitable for solving problems involving a high variability in time or space.[20][21]

Finite volume method

The finite volume method is also similar to the finite element method. It also subdivides the object of interest into smaller volumes (or elements), then the physical quantities are solved over the control volume as fluxes of these quantities across the different faces.[2][22] The equations used are usually based on the conservation or balance of physical quantities, like mass and energy.[22][23]

The finite volume method can be applied on irregular meshes like the finite element method. The element equations are still physically meaningful. However, it is difficult to get better accuracy, as the higher order version of element equations are not well-defined.[2][22][23]

Finite difference method

The finite difference method approximates differential equations by approximating the derivative with a difference equation, which is the major method to solve partial differential equations.[24][25][26][27]

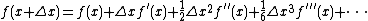
and

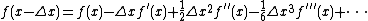
Summing up the above expressions:[28]

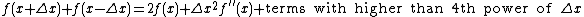
Ignore the terms with higher than 4th power of , then:[28]

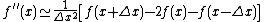
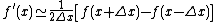
The above is the central-difference approximation of the derivatives,[28] which can also be approximated by forward-difference:

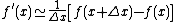
or backward-difference:

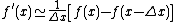
The accuracy of the finite differences can be improved when more higher order terms are used.

Discrete element method

The discrete element method, sometimes called distinct element method, is usually used to model discontinuous materials, such as rocks with fractures like joints and bedding, since it can explicitly model the properties of discontinuities.[29] This method was developed to simulate rock mechanics problems at the beginning.[29][30]

The main idea of this method is to model the objects as an assemblage of smaller particles,[29] which is similar to building a castle out of sand. These particles are of simple geometry, such as a sphere. The physical quantities of each particle, such as velocity, are continuously updated at the contacts between them.[29] This model is relatively computationally intensive, as a large quantity of particles needs to be used,[29] especially for large-scale models, like a slope.[31] Therefore, this model is usually applied to small-scale objects.

Bonded-particle model

There are objects that are not composed of granular materials, such as crystalline rocks composed of mineral grains that stick to each other or interlock with each other. Some bonding between particles is added to model this cohesion or cementation between particles. This kind of model is also called a bonded-particle model.[32][33][34]

Applications

Numerical modeling can be used to model problems in different fields of geology at various scales, such as engineering geology, geophysics, geomechanics, geodynamics, rock mechanics, and hydrogeology. The following are some examples of applications of numerical modeling in geology.

Specimen to outcrop scale

Rock mechanics

Numerical modeling has been widely applied in different fields of rock mechanics.[35] Rock is a material that is difficult to model because rock are usually:[35]

  • Discontinuous: There are numerous fractures and micro-fractures in a rock mass[36] and the space in the rock mass maybe filled with other substances like air and water.[35] A complex model is needed to fully capture these discontinuities, since the discontinuities have great effects on the rock mass.[35]
  • Anisotropic: The properties of rock mass, such as permeability (the ability to allow fluid to flow through), may vary in different directions.[35][36]
  • Inhomogeneous: The properties of different portions of the rock mass may be different.[35][36] For example, the physical properties of quartz grains and feldspar grains are different in granite.[37][38]
  • Not elastic: Rock cannot perfectly revert to its original shape after stress is removed.[36][35]

In order to model the behaviors of rock, a complex model that takes all the above characteristics into account is needed.[35] There are many models modeling rock as a continuum using methods like finite difference, finite element, and boundary element methods. One of the disadvantages is that the ability of modeling cracks and other discontinuities is usually limited in these models.[39] Models that model rock as a discontinuum, using methods like discrete element and discrete fracture network methods, are also commonly employed.[35][34] Combinations of both methods have also been developed.[35]

Numerical modeling enhances the understanding of mechanical processes in rock by conducting numerical experiments, and is useful for design and construction works.[35]

Regional-scale

Thermochronology

Numerical modeling has been used to predict and describe the thermal history of the Earth's crust, which allows geologists to improve their interpretation of thermochronological data.[130] Thermochronology can indicate the time at which a rock cooled below a particular temperature.[40] Geologic events, like the development of a faults and surface erosion, can change the thermochronological pattern of samples collected on the surface, and it is possible to constrain the geologic events by these data.[40] Numerical modeling can be used to predict the pattern.

The difficulties of thermal modeling of the Earth's crust mainly involve the irregularity and the changes of the Earth's surface (mainly erosion) through time. Therefore, in order to model the morphological changes of the Earth's surface, the models need to solve heat equations with boundary conditions that change with time and have irregular meshes.[41]

Pecube

Pecube is one of the numerical models developed to predict the thermochronological pattern.[41] It solves the following generalized heat transfer equation with advection using finite element method.[42] The first three terms on the right-hand side are the heat transferred by conduction in , and directions while is the advection.

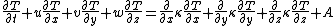
After the temperature field is constructed in the model, particle paths are traced and the cooling history of the particles can be obtained.[42] The pattern of thermochronological age can then be computed.[42]

Hydrogeology

{{See also|Groundwater model}}

In hydrogeology, groundwater flow is often modeled numerically by the finite element method[45][46][47] and finite difference method.[48] These two methods have been shown to produce similar results if the mesh is fine enough.[49][50]

MODFLOW

One of the well-known programs in modeling groundwater flow is MODFLOW, developed by the United States Geological Survey. It is a free and open-source program that uses the finite difference method as the framework to model groundwater conditions. The recent development of related programs offers more features, including:[51][52]

  • Interactions between groundwater and surface-water systems[51]
  • Transportation of solutes[51]
  • Flow of fluid with variable density, such as salt water[51]
  • Compaction of aquifer systems[51]
  • Subsidence of land[51]
  • Management of groundwater[51]

Crustal dynamics

The rheology (response of materials to stress) of crust and the lithosphere is complex, since a free surface (the land surface) and the plasticity and elasticity of the crustal materials need to be considered.[2] Most of the models use finite element methods with a Lagrangian mesh.[2] One usage is the study of deformation and kinematics of subduction.[160][53]

FLAC

The Fast Lagrangian Analysis of Continua (FLAC) is one of the most popular approaches in modeling crustal dynamics.[2] The approach is fast as it solves the equations of momentum and continuity without using a matrix, hence it is fast but time steps must be small enough.[54] The approach has been used in 2D,[55][56][57] 2.5D,[58] and 3D[59] studies of crustal dynamics, in which the 2.5D results were generated by combining multiple slices of two-dimensional results.[2]

Global-scale

Mantle convection

Finite element,[64] finite volume, finite difference[65] and spectral methods have all been used in modeling mantle convection, and almost every model used an Eulerian grid.[2] Due to the simplicity and speed of the finite-difference and spectral methods, they were used in some early models, but finite-element or finite volume methods were generally adopted in the 2010s.[2] Many benchmark papers have investigated the validity of these numerical models.[2][66][67][68][69][70][71] Current approaches mostly uses a fixed and uniform grid.[2] Grid refinement, in which the size of the elements is reduced in the part that requires more accurate approximation, is possibly the direction of future development in numerical modeling of mantle convection.[2][72]
Finite difference approach

In the 1960s to 1970s, mantle convection models using the finite difference approach usually used second-order finite differences.[2][66] Stream functions were used to remove the effect of pressure and reduce the complexity of the algorithm.[2] Due to the advancement in computer technology, finite differences with higher order terms are now used to generate a more accurate result.[2][73]

Finite volume approach

Mantle convection modeled by finite volume approach is often based on the balance between pressure and momentum. The equations derived are the same as the finite difference approach using a grid with staggered velocity and pressure, in which the values of velocity and the pressure of each element are located at different points.[2] This approach can maintain the coupling between velocity and pressure.[2]

Multiple codes are developed based on this finite difference/finite volume approach.[2][74][75][76][77][65][78] In modeling three-dimensional geometry of the Earth, since the parameters of mantles vary at different scales, multigrid, which means using different grid sizes for different variables, is applied to overcome the difficulties.[2] Examples include the cubed sphere grid,[79][80] 'Yin-Yang' grid,[81][82][83] and spiral grid.[84]

Finite element approach

In the finite element approach, stream functions are also often used to reduce the complexity of the equations.[2] ConMan,[85] modeling two-dimensional incompressible flow in the mantle, was one of the popular codes for modeling mantle convection in the 1990s.[86][2] Citcom, an Eulerian mutlgrid finite element model, is one of the most popular programs[2] to model mantle convection in 2D[87] and 3D.[88]

Spectral method

The spectral method in mantle convection breaks down the three-dimensional governing equation into several one-dimensional equations, which solves the equations much faster. It was one of the popular approaches in early models of mantle convection.[2] Many program were developed using this method during the 1980s to early 2000s.[2][89][90][91][92][93][94][95] However, the lateral changes of viscosity of mantle are difficult to manage in this approach, and other methods became more popular in the 2010s.[2]

Plate tectonics

Plate tectonics is a theory suggesting that the Earth's lithosphere is essentially composed of plates floating on the mantle.[96] The mantle convection model is fundamental in modeling the plates floating on it, and there are two major approaches to incorporate the plates into this model: rigid-block approach and rheological approach.[2] The rigid-block approach assumes the plates are rigid, which means the plates keep their shape and do not deform, just like some wooden blocks floating on water. In contrast, the rheological approach models the plates as a highly viscous fluid in which the equations applied to the lithosphere beneath also apply to the plates on top.[2]

Geodynamo

Numerical models have been made to verify the geodynamo theory, a theory that posits that the geomagnetic field is generated by the motion of conductive iron and nickel fluid in the Earth's core.[2][97]

Modeling of the flow of Earth's liquid outer core is difficult because:[2]

  • the Coriolis effect due to the Earth's rotation cannot be ignored
  • the magnetic field generated will also generate Lorentz force, which will affect the motion of the conductive fluid in the liquid outer core
  • the low viscosity of liquid iron makes the fluid flow hard to model

Most of the models use the spectral method to simulate the geodynamo,[2][98] for example the Glatzmaier-Roberts model.[99][100] Finite difference method has also been used in the model by Kageyama and Sato.[98][101] Some study also tried other methods, like finite volume[102] and finite element methods.[103]

Seismology

Finite difference methods have been widely used in simulations of the propagation of seismic waves.[105][106][107] However, due to limitations in computation power, in some models, the spacing of the mesh is too large (compared with the wavelength of the seismic waves) so that the results are inaccurate due to grid dispersion, in which the seismic waves with different frequencies separate.[105][108] Some researchers suggest using the spectral method to model seismic wave propagation.[105][109]

Errors and limitations

Sources of error

While numerical modeling provides accurate quantitative estimation to geological problems, there is always a difference between the actual observation and the modeling results due to:[2]

  • the simplification of the actual problem when building the numerical model.[2] Since numerous factors can affect a geological system, it is nearly impossible to take everything into account. Therefore, a numerical model usually simplifies the actual system by omitting the less significant factors. For instance, the Earth is often modeled as a sphere, despite the undulation of Earth's surface.
  • the approximations or idealizations of the governing equations.[2] Many objects in nature are complex. It is impossible to capture all the characteristics using equations. For instance, rocks are discontinuous, but modeling rock as a continuous material is reasonable at large scale as it describes the properties accurately enough.
  • the approximations in the discretization process.[2] Since the governing equations in the model cannot be solved directly, approximations to these equations are made using discretization and numerical methods.
  • the uncertainty in physical parameters.[2] For example, the models of the viscosity of mantle and core are not accurate.[110]

Limitations

Apart from the errors, there are some limitations in using numerical models:

  • Users of the models need a high level of knowledge and experience to prevent misuse and misinterpretation of results.[111]

See also

{{Wikibooks|Introduction to Numerical Methods}}
  • Geologic modeling
  • Numerical analysis

References

1. ^1 {{Cite web|url=https://www.nsf.gov/news/news_summ.jsp?cntn_id=121763&org=NSF|title=Stampede Charges Computational Science Forward in Tackling Complex Societal Challenges|last=|first=|date=|website=|archive-url=|archive-date=|dead-url=|access-date=}}
2. ^1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 {{cite book|title=Computational methods for geodynamics|last1=Ismail-Zadeh|first1=A.|last2=Tackley|first2=P.|date=2010|publisher=Cambridge University Press}}
3. ^{{Cite journal|last=Koyi|first=H.|date=1997-04-01|title=Analogue Modelling: From a Qualitative to a Quantitative Technique — a Historical Outline|journal=Journal of Petroleum Geology|language=en|volume=20|issue=2|pages=223–238|doi=10.1111/j.1747-5457.1997.tb00774.x|issn=1747-5457|bibcode=1997JPetG..20..223K}}
4. ^1 {{cite journal|last1=Barnichon|first1=J. D.|date=1998|title=Finite element modelling in structural and petroleum geology|url=http://bictel.ulg.ac.be/ETD-db/collection/available/ULgetd-12052007-100755/unrestricted/These_Barnichon.pdf}}
5. ^{{cite journal|last1=Malavieille|first1=J.|date=1984|title=Modélisation expérimentale des chevauchements imbriqués : application aux chaines de montagnes|url=https://www.researchgate.net/publication/276318347|journal=Bulletin de la Société Géologique de France|volume=XXVI|issue=1|pages=129–138}}
6. ^{{Cite journal|last1=Zhong|first1=S.|last2=Yuen|first2=D. A.|last3=Moresi|first3=L. N.|last4=Schubert|first4=G|date=2007|title=Numerical methods for mantle convection|url=|journal=Treatise in Geophysics|volume=|pages=|via=}}
7. ^{{Cite journal|last=PARRISH|first=D.K.|date=1973|title=A non-linear finite element fold model|url=|journal=American Journal of Science|volume=273|issue=4|pages=318–334|via=|bibcode=1973AmJS..273..318P|doi=10.2475/ajs.273.4.318|hdl=1911/14887}}
8. ^{{Cite journal|last=De Bremaecker|first=J. -Cl.|last2=Becker|first2=Eric B.|date=1978-10-10|title=Finite element models of folding|url=http://www.sciencedirect.com/science/article/pii/0040195178901427|journal=Tectonophysics|volume=50|issue=2|pages=349–367|doi=10.1016/0040-1951(78)90142-7|bibcode=1978Tectp..50..349D}}
9. ^{{Cite journal|last=Turcotte|first=D. L.|last2=Torrance|first2=K. E.|last3=Hsui|first3=A. T.|date=1973|title=Convection in the earth's mantle|journal=In: Methods in Computational Physics. Volume 13. New York|bibcode=1973mcpr...13..431T|volume=13|pages=431–454}}
10. ^{{Cite journal|last=Ranalli|first=Giorgio|title=Experimental tectonics: from Sir James Hall to the present|journal=Journal of Geodynamics|volume=32|issue=1–2|pages=65–76|doi=10.1016/s0264-3707(01)00023-0|bibcode=2001JGeo...32...65R|year=2001}}
11. ^1 {{Cite book|url=https://www.springer.com/la/book/9783540420743|title=Computational Methods for Fluid Dynamics {{!}} Joel H. Ferziger {{!}} Springer|language=en|isbn=9783540420743|publisher=Springer|year=2002}}
12. ^{{Cite journal|last=Polyanin|first=Andrei|last2=Schiesser|first2=William|last3=Zhurov|first3=Alexei|date=2008-10-10|title=Partial differential equation|journal=Scholarpedia|language=en|volume=3|issue=10|pages=4605|doi=10.4249/scholarpedia.4605|issn=1941-6016|bibcode=2008SchpJ...3.4605P}}
13. ^1 2 {{Cite book|title=An Introduction to Fluid Dynamics|last=Batchelor|first=G. K.|date=2000-02-28|publisher=Cambridge University Press|isbn=9780521663960|language=en}}
14. ^{{Cite journal|last=Ghosh|first=Somnath|last2=Kikuchi|first2=Noboru|title=An arbitrary Lagrangian-Eulerian finite element method for large deformation analysis of elastic-viscoplastic solids|journal=Computer Methods in Applied Mechanics and Engineering|volume=86|issue=2|pages=127–188|doi=10.1016/0045-7825(91)90126-q|bibcode=1991CMAME..86..127G|year=1991}}
15. ^1 {{Cite journal|last=Hu|first=Y.|last2=Randolph|first2=M. F.|date=1998-05-01|title=A practical numerical approach for large deformation problems in soil|url=http://onlinelibrary.wiley.com/doi/10.1002/(SICI)1096-9853(199805)22:53.0.CO;2-X/abstract|journal=International Journal for Numerical and Analytical Methods in Geomechanics|language=en|volume=22|issue=5|pages=327–350|doi=10.1002/(sici)1096-9853(199805)22:5<327::aid-nag920>3.0.co;2-x|issn=1096-9853}}
16. ^1 2 3 {{Cite book|title=Introduction to numerical geodynamic modelling|last=Taras.|first=Gerya|date=2010|publisher=Cambridge University Press|isbn=9780521887540|location=Cambridge, UK|oclc=664028049}}
17. ^{{Cite journal|last=Atkinson|first=Kendall|date=2007-08-29|title=Numerical analysis|journal=Scholarpedia|language=en|volume=2|issue=8|pages=3163|doi=10.4249/scholarpedia.3163|issn=1941-6016|bibcode=2007SchpJ...2.3163A}}
18. ^1 {{Cite journal|last=Oden|first=J.|date=2010-05-20|title=Finite element method|journal=Scholarpedia|language=en|volume=5|issue=5|pages=9836|doi=10.4249/scholarpedia.9836|issn=1941-6016|bibcode=2010SchpJ...5.9836O}}
19. ^1 2 3 4 5 6 7 8 9 10 11 12 {{Cite book|title=A First Course in the Finite Element Method|last=Logan|first=Daryl L.|date=2016-01-01|publisher=Cengage Learning|isbn=9781305635111|language=en}}
20. ^1 2 3 4 {{Cite book|title=Chebyshev and Fourier Spectral Methods: Second Revised Edition|last=Boyd|first=John P.|date=2001-12-03|publisher=Courier Corporation|isbn=9780486411835|language=en}}
21. ^1 2 3 4 {{Cite journal|last=Gottlieb|first=David|last2=Gottlieb|first2=Sigal|author2-link=Sigal Gottlieb|date=2009-09-02|title=Spectral methods|journal=Scholarpedia|language=en|volume=4|issue=9|pages=7504|doi=10.4249/scholarpedia.7504|issn=1941-6016|bibcode=2009SchpJ...4.7504G}}
22. ^1 2 {{Cite book|chapter-url=http://www.sciencedirect.com/science/article/pii/S1570865900070058|title=Handbook of Numerical Analysis|last=Eymard|first=Robert|last2=Gallouët|first2=Thierry|last3=Herbin|first3=Raphaèle|date=2000-01-01|publisher=Elsevier|series=Solution of Equation in ℝ (Part 3), Techniques of Scientific Computing (Part 3)|volume=7|pages=713–1018|doi=10.1016/S1570-8659(00)07005-8|chapter=Finite volume methods|isbn=9780444503503}}
23. ^1 {{Cite journal|last=Eymard|first=Robert|last2=Gallouët|first2=Thierry|last3=Herbin|date=2010-06-23|title=Finite volume method|journal=Scholarpedia|language=en|volume=5|issue=6|pages=9835|doi=10.4249/scholarpedia.9835|issn=1941-6016|bibcode=2010SchpJ...5.9835E}}
24. ^{{Cite journal|last=Fornberg|first=Bengt|date=2011-10-19|title=Finite difference method|journal=Scholarpedia|language=en|volume=6|issue=10|pages=9685|doi=10.4249/scholarpedia.9685|issn=1941-6016|bibcode=2011SchpJ...6.9685F}}
25. ^{{Cite book|url=https://www.springer.com/la/book/9783540715825|title=Numerical Treatment of Partial Differential Equations {{!}} Christian Grossmann {{!}} Springer|language=en|isbn=9783540715825|publisher=Springer|year=2007|series=Universitext}}
26. ^{{Cite book|title=Finite Difference Methods for Ordinary and Partial Differential Equations|date=2007-01-01|publisher=Society for Industrial and Applied Mathematics|isbn=9780898716290|series=Other Titles in Applied Mathematics|pages=285–310|doi=10.1137/1.9780898717839.appd|chapter = D. Matrix Powers and Exponentials}}
27. ^{{Cite book|title=Numerical Solution of Partial Differential Equations: An Introduction|last=Morton|first=K. W.|last2=Mayers|first2=D. F.|date=2005-04-11|publisher=Cambridge University Press|isbn=9781139443203|language=en}}
28. ^1 2 3 {{Cite book|title=Numerical Solution of Partial Differential Equations: Finite Difference Methods|last=Smith|first=Gordon D.|date=1985|publisher=Clarendon Press|isbn=9780198596509|language=en}}
29. ^1 2 3 4 5 {{Cite journal|last=Jing|first=L.|last2=Hudson|first2=J. A.|date=2002-06-01|title=Numerical methods in rock mechanics|journal=International Journal of Rock Mechanics and Mining Sciences|series=Numerical Methods in Rock Mechanics|volume=39|issue=4|pages=409–427|doi=10.1016/S1365-1609(02)00065-5}}
30. ^{{Cite journal|last=CUNDALL|first=P. A.|date=1971|title=A computer model for simulating progressive, large scale movement in blocky rock systems|url=http://ci.nii.ac.jp/naid/10003097768/|journal=Symp. ISRM, Nancy, France, Proc.|volume=2|pages=129–136}}
31. ^{{Cite journal|last=Cundall|first=P. A.|date=2001-01-01|title=A discontinuous future for numerical modelling in geomechanics?|journal=Proceedings of the Institution of Civil Engineers – Geotechnical Engineering|volume=149|issue=1|pages=41–47|doi=10.1680/geng.2001.149.1.41|issn=1353-2618}}
32. ^{{Cite journal|last=Potyondy|first=D. O.|last2=Cundall|first2=P. A.|date=2004-12-01|title=A bonded-particle model for rock|journal=International Journal of Rock Mechanics and Mining Sciences|series=Rock Mechanics Results from the Underground Research Laboratory, Canada|volume=41|issue=8|pages=1329–1364|doi=10.1016/j.ijrmms.2004.09.011}}
33. ^{{Cite journal|last=Zhang|first=Xiao-Ping|last2=Wong|first2=Louis Ngai Yuen|date=2013-09-01|title=Crack Initiation, Propagation and Coalescence in Rock-Like Material Containing Two Flaws: a Numerical Study Based on Bonded-Particle Model Approach|journal=Rock Mechanics and Rock Engineering|language=en|volume=46|issue=5|pages=1001–1021|doi=10.1007/s00603-012-0323-1|issn=0723-2632|bibcode=2013RMRE...46.1001Z}}
34. ^1 {{Cite journal|last=Zhang|first=Xiao-Ping|last2=Wong|first2=Louis Ngai Yuen|date=2012-09-01|title=Cracking Processes in Rock-Like Material Containing a Single Flaw Under Uniaxial Compression: A Numerical Study Based on Parallel Bonded-Particle Model Approach|journal=Rock Mechanics and Rock Engineering|language=en|volume=45|issue=5|pages=711–737|doi=10.1007/s00603-011-0176-z|issn=0723-2632|bibcode=2012RMRE...45..711Z}}
35. ^1 2 3 4 5 6 7 8 9 10 11 {{Cite journal|last=Jing|first=L.|title=A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering|journal=International Journal of Rock Mechanics and Mining Sciences|volume=40|issue=3|pages=283–353|doi=10.1016/s1365-1609(03)00013-3|year=2003}}
36. ^1 2 3 {{Cite book|title=Engineering Rock Mechanics: Part 2: Illustrative Worked Examples|last=Harrison|first=John P.|date=2001-01-26|publisher=Elsevier|isbn=9780080530932|language=en}}
37. ^{{Cite web|url=https://www.mindat.org/min-3337.html|title=Quartz: Quartz mineral information and data.|website=www.mindat.org|access-date=2017-11-17}}
38. ^{{Cite web|url=https://www.mindat.org/min-1624.html|title=Feldspar Group: Feldspar Group mineral information and data.|website=www.mindat.org|access-date=2017-11-17}}
39. ^{{Cite journal|last=Wu|first=Zhijun|last2=Wong|first2=Louis Ngai Yuen|title=Frictional crack initiation and propagation analysis using the numerical manifold method|journal=Computers and Geotechnics|volume=39|pages=38–53|doi=10.1016/j.compgeo.2011.08.011|year=2012}}
40. ^1 {{Cite journal|last=Reiners|first=Peter W.|last2=Ehlers|first2=Todd A.|last3=Zeitler|first3=Peter K.|date=2005-01-01|title=Past, Present, and Future of Thermochronology|journal=Reviews in Mineralogy and Geochemistry|language=en|volume=58|issue=1|pages=1–18|doi=10.2138/rmg.2005.58.1|issn=1529-6466|bibcode=2005RvMG...58....1R}}
41. ^1 2 3 4 {{Cite journal|last=Braun|first=Jean|date=2003-07-01|title=Pecube: a new finite-element code to solve the 3D heat transport equation including the effects of a time-varying, finite amplitude surface topography|journal=Computers & Geosciences|volume=29|issue=6|pages=787–794|doi=10.1016/S0098-3004(03)00052-9|bibcode=2003CG.....29..787B}}
42. ^1 2 3 {{Cite journal|last=Braun|first=Jean|last2=van der Beek|first2=Peter|last3=Valla|first3=Pierre|last4=Robert|first4=Xavier|last5=Herman|first5=Frédéric|last6=Glotzbach|first6=Christoph|last7=Pedersen|first7=Vivi|last8=Perry|first8=Claire|last9=Simon-Labric|first9=Thibaud|date=2012-02-20|title=Quantifying rates of landscape evolution and tectonic processes by thermochronology and numerical modeling of crustal heat transport using PECUBE|journal=Tectonophysics|volume=524|issue=Supplement C|pages=1–28|doi=10.1016/j.tecto.2011.12.035|bibcode=2012Tectp.524....1B}}
43. ^1 {{Cite journal|last=Braun|first=Jean|last2=Beek|first2=Peter van der|last3=Valla|first3=Pierre|last4=Robert|first4=Xavier|last5=Herman|first5=Frédéric|last6=Glotzbach|first6=Christoph|last7=Pedersen|first7=Vivi|last8=Perry|first8=Claire|last9=Simon-Labric|first9=Thibaud|title=Quantifying rates of landscape evolution and tectonic processes by thermochronology and numerical modeling of crustal heat transport using PECUBE|journal=Tectonophysics|volume=524–525|pages=1–28|doi=10.1016/j.tecto.2011.12.035|bibcode=2012Tectp.524....1B|year=2012}}
44. ^{{Cite journal|last=Coutand|first=Isabelle|last2=Whipp|first2=David M.|last3=Grujic|first3=Djordje|last4=Bernet|first4=Matthias|last5=Fellin|first5=Maria Giuditta|last6=Bookhagen|first6=Bodo|last7=Landry|first7=Kyle R.|last8=Ghalley|first8=S. K.|last9=Duncan|first9=Chris|date=2014-02-01|title=Geometry and kinematics of the Main Himalayan Thrust and Neogene crustal exhumation in the Bhutanese Himalaya derived from inversion of multithermochronologic data|journal=Journal of Geophysical Research: Solid Earth|language=en|volume=119|issue=2|pages=2013JB010891|doi=10.1002/2013JB010891|issn=2169-9356|bibcode=2014JGRB..119.1446C}}
45. ^{{Cite book|title=FEFLOW: Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media|last=Diersch|first=Hans-Jörg G.|date=2013-11-22|publisher=Springer Science & Business Media|isbn=9783642387395|language=en}}
46. ^{{Cite book|title=Computational Methods in Subsurface Flow|last=Huyakorn|first=Peter S.|date=2012-12-02|publisher=Academic Press|isbn=9780323137973|language=en}}
47. ^{{Cite book|title=Finite Element Simulation in Surface and Subsurface Hydrology|last=Pinder|first=George F.|last2=Gray|first2=William G.|date=2013-09-03|publisher=Elsevier|isbn=9781483270425|language=en}}
48. ^{{Cite journal|last=Irwin.|first=Remson|last2=M.|first2=Hornberger, George|last3=J.|first3=Molz, Fred|date=1971|title=Numerical methods in subsurface hydrology|url=http://agris.fao.org/agris-search/search.do?recordID=US201300474801|journal=AGRIS: International Information System for the Agricultural Science and Technology|language=English}}
49. ^{{Cite journal|last=Pinder|first=George F.|last2=Gray|first2=William G.|date=1976-02-01|title=Is there a difference in the finite element method?|journal=Water Resources Research|language=en|volume=12|issue=1|pages=105–107|doi=10.1029/WR012i001p00105|issn=1944-7973|bibcode=1976WRR....12..105P}}
50. ^{{Cite book|title=Applied Groundwater Modeling: Simulation of Flow and Advective Transport|last=Anderson|first=Mary P.|last2=Woessner|first2=William W.|last3=Hunt|first3=Randall J.|date=2015-08-13|publisher=Academic Press|isbn=9780080916385|language=en}}
51. ^1 2 3 4 5 6 {{Cite web|url=https://water.usgs.gov/ogw/modflow/new-start-here.html|title=Information for New MODFLOW Users|last=Groundwater|first=USGS – U.S. Geological Survey Office of|website=water.usgs.gov|language=en|access-date=2017-10-12}}
52. ^{{Cite journal|last=McDonald|first=Michael G.|last2=Harbaugh|first2=Arlen W.|last3=the original authors of MODFLOW|date=2003-03-01|title=The History of MODFLOW|journal=Ground Water|language=en|volume=41|issue=2|pages=280–283|doi=10.1111/j.1745-6584.2003.tb02591.x|issn=1745-6584}}
53. ^{{Cite journal|last=Liao|first=Jie|last2=Gerya|first2=Taras|last3=Thielmann|first3=Marcel|last4=Webb|first4=A. Alexander G.|last5=Kufner|first5=Sofia-Katerina|last6=Yin|first6=An|title=3D geodynamic models for the development of opposing continental subduction zones: The Hindu Kush–Pamir example|journal=Earth and Planetary Science Letters|volume=480|pages=133–146|doi=10.1016/j.epsl.2017.10.005|bibcode=2017E&PSL.480..133L|year=2017}}
54. ^{{Cite journal|last=Cundall|first=P. A.|date=1989-03-01|title=Numerical experiments on localization in frictional materials|journal=Ingenieur-Archiv|language=en|volume=59|issue=2|pages=148–159|doi=10.1007/BF00538368|issn=0020-1154}}
55. ^{{Cite journal|last=Poliakov|first=A. N. B|last2=van Balen|first2=R|last3=Podladchikov|first3=Yu|last4=Daudre|first4=B|last5=Cloetingh|first5=S|last6=Talbot|first6=C|date=1993-11-15|title=Numerical analysis of how sedimentation and redistribution of surficial sediments affects salt diapirism|url=http://www.sciencedirect.com/science/article/pii/0040195193901184|journal=Tectonophysics|series=The origin of sedimentary basins: Inferences from quantitative modelling and basin analysis|volume=226|issue=1|pages=199–216|doi=10.1016/0040-1951(93)90118-4|bibcode=1993Tectp.226..199P}}
56. ^{{Cite journal|last=Poliakov|first=A. N. B.|last2=Podladchikov|first2=Yu.|last3=Talbot|first3=C.|date=1993-12-30|title=Initiation of salt diapirs with frictional overburdens: numerical experiments|url=http://www.sciencedirect.com/science/article/pii/004019519390341G|journal=Tectonophysics|volume=228|issue=3|pages=199–210|doi=10.1016/0040-1951(93)90341-G|bibcode=1993Tectp.228..199P}}
57. ^{{Cite book|title=Flow and Creep in the Solar System: Observations, Modeling and Theory|last=Poliakov|first=A. N. B.|last2=Cundall|first2=P. A.|last3=Podladchikov|first3=Y. Y.|last4=Lyakhovsky|first4=V. A.|date=1993|publisher=Springer, Dordrecht|isbn=9789048142453|series=NATO ASI Series|pages=175–195|language=en|doi=10.1007/978-94-015-8206-3_12}}
58. ^{{Cite journal|last=Sobolev|first=S. V.|last2=Petrunin|first2=A.|last3=Garfunkel|first3=Z.|last4=Babeyko|first4=A. Y.|date=2005-09-30|title=Thermo-mechanical model of the Dead Sea Transform|journal=Earth and Planetary Science Letters|volume=238|issue=1|pages=78–95|doi=10.1016/j.epsl.2005.06.058|bibcode=2005E&PSL.238...78S}}
59. ^{{Cite journal|last=Choi|first=Eun-seo|last2=Lavier|first2=Luc|last3=Gurnis|first3=Michael|date=2008-12-01|title=Thermomechanics of mid-ocean ridge segmentation|journal=Physics of the Earth and Planetary Interiors|series=Recent Advances in Computational Geodynamics: Theory, Numerics and Applications|volume=171|issue=1|pages=374–386|doi=10.1016/j.pepi.2008.08.010|bibcode=2008PEPI..171..374C}}
60. ^{{Cite journal|last=Wang|first=Yuejun|last2=Zhang|first2=Feifei|last3=Fan|first3=Weiming|last4=Zhang|first4=Guowei|last5=Chen|first5=Shiyue|last6=Cawood|first6=Peter A.|last7=Zhang|first7=Aimei|date=2010-12-01|title=Tectonic setting of the South China Block in the early Paleozoic: Resolving intracontinental and ocean closure models from detrital zircon U-Pb geochronology|journal=Tectonics|language=en|volume=29|issue=6|pages=TC6020|doi=10.1029/2010TC002750|issn=1944-9194|bibcode=2010Tecto..29.6020W}}
61. ^1 2 3 4 5 6 {{Cite journal|last=Zuo|first=Xuran|last2=Chan|first2=Lung Sang|last3=Gao|first3=Jian-Feng|date=2017-02-09|title=Compression-extension transition of continental crust in a subduction zone: A parametric numerical modeling study with implications on Mesozoic-Cenozoic tectonic evolution of the Cathaysia Block|journal=PLOS ONE|volume=12|issue=2|pages=e0171536|doi=10.1371/journal.pone.0171536|pmid=28182640|pmc=5300286|issn=1932-6203|bibcode=2017PLoSO..1271536Z}}
62. ^1 2 {{Cite journal|last=Wolfgang|first=Bangerth|last2=Juliane|first2=Dannberg|last3=Rene|first3=Gassmoeller|last4=Timo|first4=Heister|last5=others|date=2017-04-12|title=ASPECT: Advanced Solver for Problems in Earth's ConvecTion, User Manual|url=https://figshare.com/articles/ASPECT_Advanced_Solver_for_Problems_in_Earth_s_ConvecTion_User_Manual/4865333|journal=Figshare|language=en-US|doi=10.6084/m9.figshare.4865333}}
63. ^{{Cite journal|last=Kronbichler|first=Martin|last2=Heister|first2=Timo|last3=Bangerth|first3=Wolfgang|date=2012-10-01|title=High accuracy mantle convection simulation through modern numerical methods|journal=Geophysical Journal International|volume=191|issue=1|pages=12–29|doi=10.1111/j.1365-246x.2012.05609.x|issn=0956-540X|bibcode=2012GeoJI.191...12K}}
64. ^{{Cite journal|last=Stadler|first=Georg|last2=Gurnis|first2=Michael|last3=Burstedde|first3=Carsten|last4=Wilcox|first4=Lucas C.|last5=Alisic|first5=Laura|last6=Ghattas|first6=Omar|date=2010-08-27|title=The Dynamics of Plate Tectonics and Mantle Flow: From Local to Global Scales|journal=Science|language=en|volume=329|issue=5995|pages=1033–1038|doi=10.1126/science.1191223|issn=0036-8075|pmid=20798311|bibcode=2010Sci...329.1033S}}
65. ^1 {{Cite journal|last=Gerya|first=Taras V.|last2=Yuen|first2=David A.|date=2003-12-30|title=Characteristics-based marker-in-cell method with conservative finite-differences schemes for modeling geological flows with strongly variable transport properties|journal=Physics of the Earth and Planetary Interiors|volume=140|issue=4|pages=293–318|doi=10.1016/j.pepi.2003.09.006|bibcode=2003PEPI..140..293G}}
66. ^1 {{Cite journal|last=Blankenbach|first=B.|last2=Busse|first2=F.|last3=Christensen|first3=U.|last4=Cserepes|first4=L.|last5=Gunkel|first5=D.|last6=Hansen|first6=U.|last7=Harder|first7=H.|last8=Jarvis|first8=G.|last9=Koch|first9=M.|date=1989-07-01|title=A benchmark comparison for mantle convection codes|journal=Geophysical Journal International|language=en|volume=98|issue=1|pages=23–38|doi=10.1111/j.1365-246X.1989.tb05511.x|issn=1365-246X|bibcode=1989GeoJI..98...23B}}
67. ^{{Cite journal|last=Travis|first=B. J.|last2=Anderson|first2=C.|last3=Baumgardner|first3=J.|last4=Gable|first4=C. W.|last5=Hager|first5=B. H.|last6=O'Connell|first6=R. J.|last7=Olson|first7=P.|last8=Raefsky|first8=A.|last9=Schubert|first9=G.|date=1990-12-01|title=A benchmark comparison of numerical methods for infinite Prandtl number thermal convection in two-dimensional Cartesian geometry|journal=Geophysical & Astrophysical Fluid Dynamics|volume=55|issue=3–4|pages=137–160|doi=10.1080/03091929008204111|issn=0309-1929}}
68. ^{{Cite journal|last=Busse|first=F. H.|last2=Christensen|first2=U.|last3=Clever|first3=R.|last4=Cserepes|first4=L.|last5=Gable|first5=C.|last6=Giannandrea|first6=E.|last7=Guillou|first7=L.|last8=Houseman|first8=G.|last9=Nataf|first9=H. C.|date=1994-08-01|title=3D convection at infinite Prandtl number in Cartesian geometry — a benchmark comparison|journal=Geophysical & Astrophysical Fluid Dynamics|volume=75|issue=1|pages=39–59|doi=10.1080/03091929408203646|issn=0309-1929}}
69. ^{{Cite journal|last=Stemmer|first=K.|last2=Harder|first2=H.|last3=Hansen|first3=U.|date=2006-08-31|title=A new method to simulate convection with strongly temperature- and pressure-dependent viscosity in a spherical shell: Applications to the Earth's mantle|journal=Physics of the Earth and Planetary Interiors|volume=157|issue=3|pages=223–249|doi=10.1016/j.pepi.2006.04.007|bibcode=2006PEPI..157..223S}}
70. ^{{Cite journal|last=van Keken|first=P. E.|last2=King|first2=S. D.|last3=Schmeling|first3=H.|last4=Christensen|first4=U. R.|last5=Neumeister|first5=D.|last6=Doin|first6=M.-P.|date=1997-10-10|title=A comparison of methods for the modeling of thermochemical convection|journal=Journal of Geophysical Research: Solid Earth|language=en|volume=102|issue=B10|pages=22477–22495|doi=10.1029/97JB01353|issn=2156-2202|bibcode=1997JGR...10222477V}}
71. ^{{Cite journal|last=Tackley|first=Paul J.|last2=King|first2=Scott D.|date=2003-04-01|title=Testing the tracer ratio method for modeling active compositional fields in mantle convection simulations|journal=Geochemistry, Geophysics, Geosystems|language=en|volume=4|issue=4|pages=8302|doi=10.1029/2001GC000214|issn=1525-2027|bibcode=2003GGG.....4.8302T}}
72. ^{{Cite journal|last=Davies|first=D. R.|last2=Davies|first2=J. H.|last3=Hassan|first3=O.|last4=Morgan|first4=K.|last5=Nithiarasu|first5=P.|date=2007-05-01|title=Investigations into the applicability of adaptive finite element methods to two-dimensional infinite Prandtl number thermal and thermochemical convection|journal=Geochemistry, Geophysics, Geosystems|language=en|volume=8|issue=5|pages=Q05010|doi=10.1029/2006GC001470|issn=1525-2027|bibcode=2007GGG.....8.5010D|url=http://orca.cf.ac.uk/9405/1/Davies%202007.pdf}}
73. ^{{Cite journal|last=Larsen|first=Tine B.|last2=Yuen|first2=David A.|last3=Moser|first3=Jiří|last4=Fornberg|first4=Bengt|date=1997-04-01|title=A high-order finite-difference method applied to large Rayleigh number mantle convection|journal=Geophysical & Astrophysical Fluid Dynamics|volume=84|issue=1–2|pages=53–83|doi=10.1080/03091929708208973|issn=0309-1929}}
74. ^{{Cite journal|last=Trompert|first=R. A.|last2=Hansen|first2=U.|date=1996-12-01|title=The application of a finite volume multigrid method to three-dimensional flow problems in a highly viscous fluid with a variable viscosity|journal=Geophysical & Astrophysical Fluid Dynamics|volume=83|issue=3–4|pages=261–291|doi=10.1080/03091929608208968|issn=0309-1929}}
75. ^{{Cite journal|last=Auth|first=C.|last2=Harder|first2=H.|date=1999-06-01|title=Multigrid solution of convection problems with strongly variable viscosity|journal=Geophysical Journal International|language=en|volume=137|issue=3|pages=793–804|doi=10.1046/j.1365-246x.1999.00833.x|issn=0956-540X|bibcode=1999GeoJI.137..793A}}
76. ^{{Cite journal|last=Albers|first=Michael|date=2000-05-01|title=A Local Mesh Refinement Multigrid Method for 3-D Convection Problems with Strongly Variable Viscosity|journal=Journal of Computational Physics|volume=160|issue=1|pages=126–150|doi=10.1006/jcph.2000.6438|bibcode=2000JCoPh.160..126A}}
77. ^{{Cite journal|last=Kameyama|first=Masanori|last2=Kageyama|first2=Akira|last3=Sato|first3=Tetsuya|date=2005-06-10|title=Multigrid iterative algorithm using pseudo-compressibility for three-dimensional mantle convection with strongly variable viscosity|journal=Journal of Computational Physics|volume=206|issue=1|pages=162–181|doi=10.1016/j.jcp.2004.11.030|arxiv=physics/0410249|bibcode=2005JCoPh.206..162K}}
78. ^{{Cite journal|last=Gerya|first=Taras V.|last2=Yuen|first2=David A.|date=2007-08-15|title=Robust characteristics method for modelling multiphase visco-elasto-plastic thermo-mechanical problems|journal=Physics of the Earth and Planetary Interiors|series=Computational Challenges in the Earth Sciences|volume=163|issue=1|pages=83–105|doi=10.1016/j.pepi.2007.04.015|bibcode=2007PEPI..163...83G}}
79. ^{{Cite journal|last=Choblet|first=Gaël|date=2005-05-01|title=Modelling thermal convection with large viscosity gradients in one block of the 'cubed sphere'|journal=Journal of Computational Physics|volume=205|issue=1|pages=269–291|doi=10.1016/j.jcp.2004.11.005|bibcode=2005JCoPh.205..269C}}
80. ^{{Cite journal|last=Hernlund|first=John W.|last2=Tackley|first2=Paul J.|date=2008-12-01|title=Modeling mantle convection in the spherical annulus|journal=Physics of the Earth and Planetary Interiors|series=Recent Advances in Computational Geodynamics: Theory, Numerics and Applications|volume=171|issue=1|pages=48–54|doi=10.1016/j.pepi.2008.07.037|bibcode=2008PEPI..171...48H}}
81. ^{{Cite journal|last=Kageyama|first=Akira|last2=Sato|first2=Tetsuya|date=2004-09-01|title="Yin-Yang grid": An overset grid in spherical geometry|journal=Geochemistry, Geophysics, Geosystems|language=en|volume=5|issue=9|pages=Q09005|doi=10.1029/2004GC000734|issn=1525-2027|arxiv=physics/0403123|bibcode=2004GGG.....5.9005K|url=http://cds.cern.ch/record/726936|type=Submitted manuscript}}
82. ^{{Cite journal|last=Kameyama|first=Masanori|last2=Kageyama|first2=Akira|last3=Sato|first3=Tetsuya|title=Multigrid-based simulation code for mantle convection in spherical shell using Yin–Yang grid|journal=Physics of the Earth and Planetary Interiors|volume=171|issue=1–4|pages=19–32|doi=10.1016/j.pepi.2008.06.025|bibcode=2008PEPI..171...19K|year=2008}}
83. ^{{Cite journal|last=Tackley|first=Paul J.|title=Modelling compressible mantle convection with large viscosity contrasts in a three-dimensional spherical shell using the yin-yang grid|journal=Physics of the Earth and Planetary Interiors|volume=171|issue=1–4|pages=7–18|doi=10.1016/j.pepi.2008.08.005|bibcode=2008PEPI..171....7T|year=2008}}
84. ^{{Cite journal|last=Hüttig|first=Christian|last2=Stemmer|first2=Kai|date=2008-02-01|title=The spiral grid: A new approach to discretize the sphere and its application to mantle convection|journal=Geochemistry, Geophysics, Geosystems|language=en|volume=9|issue=2|pages=Q02018|doi=10.1029/2007GC001581|issn=1525-2027|bibcode=2008GGG.....9.2018H}}
85. ^{{cite web|title=Computational Infrastructure for Geodynamics :: Software|url=https://geodynamics.org/cig/software/conman/|website=geodynamics.org|language=en}}
86. ^{{Cite journal|last=King|first=Scott D.|last2=Raefsky|first2=Arthur|last3=Hager|first3=Bradford H.|date=1990-01-01|title=Conman: vectorizing a finite element code for incompressible two-dimensional convection in the Earth's mantle|url=http://www.sciencedirect.com/science/article/pii/003192019090225M|journal=Physics of the Earth and Planetary Interiors|volume=59|issue=3|pages=195–207|doi=10.1016/0031-9201(90)90225-M|bibcode=1990PEPI...59..195K}}
87. ^{{Cite journal|last=Moresi|first=L.‐N.|last2=Solomatov|first2=V. S.|date=1995-09-01|title=Numerical investigation of 2D convection with extremely large viscosity variations|journal=Physics of Fluids|volume=7|issue=9|pages=2154–2162|doi=10.1063/1.868465|issn=1070-6631|bibcode=1995PhFl....7.2154M}}
88. ^{{Cite journal|last=Moresi|first=Louis|last2=Gurnis|first2=Michael|date=1996-02-01|title=Constraints on the lateral strength of slabs from three-dimensional dynamic flow models|url=http://www.sciencedirect.com/science/article/pii/0012821X9500221W|journal=Earth and Planetary Science Letters|volume=138|issue=1|pages=15–28|doi=10.1016/0012-821X(95)00221-W|bibcode=1996E&PSL.138...15M}}
89. ^{{Cite journal|last=Frick|first=H.|last2=Busse|first2=F. H.|last3=Clever|first3=R. M.|date=1983-02-01|title=Steady three-dimensional convection at high Prandtl numbers|bibcode=1983JFM...127..141F|journal=Journal of Fluid Mechanics|volume=127|pages=141–153|doi=10.1017/S0022112083002669|issn=0022-1120}}
90. ^{{Cite journal|last=Cserepes|first=L.|last2=Rabinowicz|first2=M.|last3=Rosemberg-Borot|first3=C.|date=1988-10-10|title=Three-dimensional infinite Prandtl number convection in one and two layers with implications for the Earth's gravity field|journal=Journal of Geophysical Research: Solid Earth|language=en|volume=93|issue=B10|pages=12009–12025|doi=10.1029/JB093iB10p12009|issn=2156-2202|bibcode=1988JGR....9312009C}}
91. ^{{Cite journal|last=Gable|first=Carl W.|last2=O'Connell|first2=Richard J.|last3=Travis|first3=Bryan J.|date=1991-05-10|title=Convection in three dimensions with surface plates: Generation of toroidal flow|journal=Journal of Geophysical Research: Solid Earth|language=en|volume=96|issue=B5|pages=8391–8405|doi=10.1029/90JB02743|issn=2156-2202|bibcode=1991JGR....96.8391G}}
92. ^{{Cite journal|last=Young|first=Richard E.|date=1974|title=Finite-amplitude thermal convection in a spherical shell|url=https://www.cambridge.org/core/journals/journal-of-fluid-mechanics/article/finite-amplitude-thermal-convection-in-a-spherical-shell/D5E744D7255B27B2BABF13397D5A2C72|journal=Journal of Fluid Mechanics|volume=63|issue=4|pages=695–721|doi=10.1017/S0022112074002151|issn=1469-7645|via=|bibcode=1974JFM....63..695Y}}
93. ^{{Cite journal|last=Glatzmaier|first=Gary A.|date=1988-12-01|title=Numerical simulations of mantle convection: Time-dependent, three-dimensional, compressible, spherical shell|journal=Geophysical & Astrophysical Fluid Dynamics|volume=43|issue=2|pages=223–264|doi=10.1080/03091928808213626|issn=0309-1929}}
94. ^{{Cite journal|last=Monnereau|first=Marc|last2=Quéré|first2=Sandrine|date=2001-01-30|title=Spherical shell models of mantle convection with tectonic plates|journal=Earth and Planetary Science Letters|volume=184|issue=3|pages=575–587|doi=10.1016/S0012-821X(00)00334-4|bibcode=2001E&PSL.184..575M}}
95. ^{{Cite journal|last=Monnereau|first=Marc|last2=Quéré|first2=Sandrine|title=Spherical shell models of mantle convection with tectonic plates|journal=Earth and Planetary Science Letters|volume=184|issue=3–4|pages=575–587|doi=10.1016/s0012-821x(00)00334-4|bibcode=2001E&PSL.184..575M|year=2001}}
96. ^{{Cite book|title=Plate tectonics and crustal evolution|last=C.|first=Condie, Kent|date=1997|publisher=Butterworth Heinemann|others=Condie, Kent C.|isbn=9780750633864|edition=4th|location=Oxford|oclc=174141325}}
97. ^{{Cite book|last=Christensen|first=U.R.|last2=Wicht|first2=J.|pages=245–277|doi=10.1016/b978-0-444-53802-4.00145-7|title = Treatise on Geophysics|year = 2015|isbn = 9780444538031}}
98. ^1 {{Cite journal|last=Christensen|first=U.R.|last2=Aubert|first2=J.|last3=Cardin|first3=P.|last4=Dormy|first4=E.|last5=Gibbons|first5=S.|last6=Glatzmaier|first6=G.A.|last7=Grote|first7=E.|last8=Honkura|first8=Y.|last9=Jones|first9=C.|title=A numerical dynamo benchmark|journal=Physics of the Earth and Planetary Interiors|volume=128|issue=1–4|pages=25–34|doi=10.1016/s0031-9201(01)00275-8|bibcode=2001PEPI..128...25C|year=2001}}
99. ^{{Cite journal|last=Glatzmaier|first=Gary A.|last2=Roberts|first2=Paul H.|title=A three-dimensional convective dynamo solution with rotating and finitely conducting inner core and mantle|journal=Physics of the Earth and Planetary Interiors|volume=91|issue=1–3|pages=63–75|doi=10.1016/0031-9201(95)03049-3|bibcode=1995PEPI...91...63G|year=1995}}
100. ^{{Cite book|title=Magnetohydrodynamics and the Earth's Core: Selected Works by Paul Roberts|last=Soward|first=Andrew M.|date=2002-11-28|publisher=CRC Press|isbn=9780415272223|language=en}}
101. ^{{Cite journal|last=Kageyama|first=Akira|last2=Sato|first2=Tetsuya|date=1995-05-01|title=Computer simulation of a magnetohydrodynamic dynamo. II|journal=Physics of Plasmas|volume=2|issue=5|pages=1421–1431|doi=10.1063/1.871485|issn=1070-664X|bibcode=1995PhPl....2.1421K}}
102. ^{{Cite journal|last=Helmut|first=Harder|last2=Ulrich|first2=Hansen|date=2005-05-01|title=A finite-volume solution method for thermal convection and dynamo problems in spherical shells|journal=Geophysical Journal International|language=en|volume=161|issue=2|pages=522|doi=10.1111/j.1365-246X.2005.02560.x|issn=0956-540X|bibcode=2005GeoJI.161..522H}}
103. ^{{Cite journal|last=Chan|first=Kit H.|last2=Zhang|first2=Keke|last3=Li|first3=Ligang|last4=Liao|first4=Xinhao|title=A new generation of convection-driven spherical dynamos using EBE finite element method|journal=Physics of the Earth and Planetary Interiors|volume=163|issue=1–4|pages=251–265|doi=10.1016/j.pepi.2007.04.017|bibcode=2007PEPI..163..251C|year=2007}}
104. ^{{Cite web|url=https://websites.pmc.ucsc.edu/~glatz/geodynamo.html|title=Geodynamo|website=websites.pmc.ucsc.edu|access-date=2017-10-13}}
105. ^1 2 {{Cite journal|last=Komatitsch|first=Dimitri|last2=Vilotte|first2=Jean-Pierre|date=1998-04-01|title=The spectral element method: An efficient tool to simulate the seismic response of 2D and 3D geological structures|url=https://pubs.geoscienceworld.org/bssa/article-abstract/88/2/368/120304/the-spectral-element-method-an-efficient-tool-to|journal=Bulletin of the Seismological Society of America|volume=88|issue=2|pages=368–392|issn=0037-1106}}
106. ^{{Cite journal|last=Virieux|first=J.|date=1986-04-01|title=P-SV wave propagation in heterogeneous media: Velocity‐stress finite‐difference method|journal=Geophysics|volume=51|issue=4|pages=889–901|doi=10.1190/1.1442147|issn=0016-8033|bibcode=1986Geop...51..889V}}
107. ^{{Cite journal|last=Bohlen|first=Thomas|title=Parallel 3-D viscoelastic finite difference seismic modelling|journal=Computers & Geosciences|volume=28|issue=8|pages=887–899|doi=10.1016/s0098-3004(02)00006-7|bibcode=2002CG.....28..887B|year=2002}}
108. ^{{Cite journal|last=Javaherian|first=Abdolrahim|date=1994-08-01|title=Grid dispersion in generating finite-differences synthetic seismograms|journal=Acta Seismologica Sinica|language=en|volume=7|issue=3|pages=397–407|doi=10.1007/BF02650677|issn=1000-9116|bibcode=1994AcSSn...7..397J}}
109. ^{{Cite journal|last=Komatitsch|first=Dimitri|last2=Tromp|first2=Jeroen|date=2002-07-01|title=Spectral-element simulations of global seismic wave propagation—II. Three-dimensional models, oceans, rotation and self-gravitation|journal=Geophysical Journal International|volume=150|issue=1|pages=303–318|doi=10.1046/j.1365-246X.2002.01716.x|issn=0956-540X|bibcode=2002GeoJI.150..303K}}
110. ^{{Cite journal|last=Rudolph|first=Maxwell L.|last2=Lekić|first2=Vedran|last3=Lithgow-Bertelloni|first3=Carolina|date=2015-12-11|title=Viscosity jump in Earth's mid-mantle|journal=Science|language=en|volume=350|issue=6266|pages=1349–1352|doi=10.1126/science.aad1929|issn=0036-8075|pmid=26659053|bibcode=2015Sci...350.1349R}}
111. ^{{Cite journal|last=Stead|first=D.|last2=Eberhardt|first2=E.|last3=Coggan|first3=J.S.|title=Developments in the characterization of complex rock slope deformation and failure using numerical modelling techniques|journal=Engineering Geology|volume=83|issue=1–3|pages=217–235|doi=10.1016/j.enggeo.2005.06.033|year=2006}}
{{Geology}}

1 : Geological techniques
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/12 4:51:28