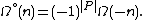- Definition
- Examples
- Reciprocity theorem
- Connections Chromatic polynomial Ehrhart polynomial Order polytope
- References
The order polynomial is a polynomial studied in mathematics, in particular in algebraic graph theory and algebraic combinatorics. The order polynomial counts the number of order-preserving maps from a poset to a chain of length  . These order-preserving maps were first introduced by Richard P. Stanley while studying ordered structures and partitions as a Ph.D. student at Harvard University in 1971 under the guidance of Gian-Carlo Rota.
. These order-preserving maps were first introduced by Richard P. Stanley while studying ordered structures and partitions as a Ph.D. student at Harvard University in 1971 under the guidance of Gian-Carlo Rota.
Definition
Let  be a finite poset,
be a finite poset,  and
and  be points in
be points in  and
and  be a chain of length
be a chain of length  . A map
. A map  is order-preserving if
is order-preserving if  implies
implies  . The number of such maps grows polynomially with
. The number of such maps grows polynomially with  , and the function that counts their number as a function of
, and the function that counts their number as a function of  is the order polynomial
is the order polynomial  .
.
Similarly, we can define an order polynomial that counts the number of strictly order-preserving maps. A map  is strictly order-preserving if
is strictly order-preserving if  implies
implies  . The order polynomial that counts the number of these maps is denoted by
. The order polynomial that counts the number of these maps is denoted by  .[1]
.[1]
Examples
Let  be a chain of length
be a chain of length  . Then
. Then  and
and 
We can also consider the poset  with
with  disjoint points. Then the number of order-preserving maps to a chain of length
disjoint points. Then the number of order-preserving maps to a chain of length  is
is  , and
, and  .
.
Reciprocity theorem
The reciprocity theorem shows that there is a relation between strictly order-preserving maps and order-preserving maps. In addition, this comes hand in hand with important properties that the chromatic polynomial and Ehrhart polynomial share. The relation can be stated as follows:[2]
In the case that  is a chain, this recovers the negative binomial identity.
is a chain, this recovers the negative binomial identity.
Connections
Chromatic polynomial
The chromatic polynomial counts the number of proper ways to color a graph. Let  be a finite graph and let
be a finite graph and let  be an acyclic orientation of
be an acyclic orientation of  . Then there is a natural binary relation on the vertices
. Then there is a natural binary relation on the vertices  of
of  defined as
defined as  if
if  . In particular,
. In particular,  is a partial ordering on the set of vertices
is a partial ordering on the set of vertices  of
of  . In addition,
. In addition,  is compatible with
is compatible with  if
if  is order-preserving. Then, we can conclude that
is order-preserving. Then, we can conclude that
where  are all acyclic orientations of G.[3]
are all acyclic orientations of G.[3]
Ehrhart polynomial
The Ehrhart polynomial is a polynomial that associates the number of integer lattice points and the expansion of a polytope  by a factor of
by a factor of  . In other words, consider the lattice
. In other words, consider the lattice  and a
and a  -dimensional polytope in
-dimensional polytope in  with integer vertices. Let
with integer vertices. Let  be a positive integer, and
be a positive integer, and  be a dilation of
be a dilation of  so
so
is the number of lattice points in  . Eugène Ehrhart showed that this was a rational polynomial of degree
. Eugène Ehrhart showed that this was a rational polynomial of degree  in
in  .[4]
.[4]
Order polytope
The order polytope associates a polytope with a partial order. Let  be a poset with
be a poset with  elements. Then the order polytope, denoted
elements. Then the order polytope, denoted  , is the set of points in the
, is the set of points in the  -dimensional unit cube such that the coordinates satisfy the partial order.[5][6]
-dimensional unit cube such that the coordinates satisfy the partial order.[5][6]
More formally, let  be the set of all functions from
be the set of all functions from  to
to  . The order polytope
. The order polytope  of the poset
of the poset  is the set of all maps
is the set of all maps  in
in  which satisfy the following two conditions. First,
which satisfy the following two conditions. First,  for all
for all  , and second,
, and second, 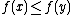 if
if  in the ordering of
in the ordering of  . Thus, the polytope can be created given a poset and a partial order.[7]
. Thus, the polytope can be created given a poset and a partial order.[7]
The volume of the order polytope is given by the leading coefficient of the order polynomial, which is the number of linear extensions of the poset  divided by
divided by  .[7][8]
.[7][8]
References
2. ^{{cite journal |last1=Stanley |first1=Richard P. |title=A chromatic-like polynomial for ordered sets |date=1970 |journal=Proc. Second Chapel Hill Conference on Combinatorial Mathematics and Its Appl. |pages=421–427}}
3. ^{{cite journal|last1=Stanley|first1=Richard P.|title=Acyclic orientations of graphs|journal=Discrete Math|date=1973|volume=5|pages=171–178}}
4. ^{{Cite book |title=Computing the continuous discretely |last=Beck |first=Matthias |last2=Robins |first2=Sinai |publisher=Springer |year=2015 |isbn=978-1-4939-2968-9 |location=New York |pages=64–72}}
5. ^{{cite journal |first1=Alexander |last1=Karzanov |first2=Leonid |last2=Khachiyan |title=On the conductance of Order Markov Chains |journal=Order |volume=8 |pages=7–15 |year=1991 |doi=10.1007/BF00385809}}
6. ^{{cite journal |first1=Graham |last1=Brightwell |first2=Peter |last2=Winkler |title=Counting linear extensions |journal=Order |volume=8 |pages=225–242 |year=1991 |doi=10.1007/BF00383444}}
7. ^1 {{Cite journal|last=Stanley|first=Richard P.|date=1986|title=Two poset polytopes|url=|journal=Discrete Comput. Geom.|doi=10.1007/BF02187680|pmid=|access-date=}}
8. ^{{cite journal|first=Nathan|last=Linial|year=1984|title=The information-theoretic bound is good for merging|journal=SIAM J. Comput.|volume=13|pages=795–801|doi=10.1137/0213049}}
{{cite journal|first1=Jeff|last1=Kahn| first2=Jeong Han|last2=Kim|title=Entropy and sorting|doi=10.1145/129712.129731|journal=Journal of Computer and System Sciences|volume=51|year=1995|pages=390–399}}
- Christenh.
- Christen Heiberg
- Christen Heiberg (physician)
- Christenhusz
- Christening font
- Christening in Tanum Church
- Christen Knudsen, Jr.
- Christen Lindencrone
- Christen, Morgan
- Christen Munk
- Christensen, Allen
- Christensen, Andrew
- Christensen, Carl
- Christensen, Christen
- Christensen, David
- Christensenella
- Christensen, Erik
- Christensen, Harald
- Christensen, Kim
- Christensen, Mads
- Christensen, Mark
- Christensen, Michael
- Christensen, Morten
- Christensen, Oliver
- Christensen, Peter