“Pinwheel scheduling”的意思、由来-开放百科全书

In mathematics and computer science, the pinwheel scheduling problem is a problem in real-time scheduling with repeating tasks of unit length and hard constraints on the time between repetitions.

Definition

The input to pinwheel scheduling consists of a list of tasks, each of which is assumed to take unit time per instantiation. Each task has an associated positive integer value, its minimum repeat time (the minimum time from the start of one instantiation of the task to the next). Only one task can be performed at any given time.{{r|hmrtv}}

The desired output is an infinite sequence specifying which task to perform in each unit of time. Each input task should appear infinitely often in the sequence, with the largest gap between two consecutive instantiations of a task at most equal to the repeat time of the task.{{r|hmrtv}}

For example, the infinitely repeating sequence abacabacabac... would be a valid pinwheel schedule for three tasks a, b, and c with repeat times that are at least 2, 4, and 4 respectively.

Density

If the task to be scheduled are numbered from

, let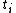

denote the repeat time for task

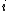. Then the density of a pinwheel scheduling problem is

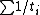. For a solution to exist, it is necessary that the density is at most

.{{r|hrtv}}

is also sufficient for a schedule to exist in the special case that all repeat times are multiples of each other (for instance, if all are powers of two), because in this case one can solve the problem using a disjoint covering system.{{r|hmrtv}} Having density at most

is also sufficient when there are exactly two distinct repeat times.{{r|hrtv}} However, it is not sufficient in other cases. In particular, there is no schedule for three items with repeat times

, and

, no matter how large

may be, even though the density of this system is only

.{{r|cc}}

Every instance of pinwheel scheduling with density at most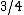

has a solution,{{r|fl}} and it has been conjectured that every instance with density at most

has a solution.{{r|cc|ll}} Every instance with three distinct repeat times and density at most

does have a solution.{{r|ll}}

Periodicity and complexity

When there exists a solution, the solution can be assumed to be periodic, with a period at most equal to the product of the repeat times. However, it is not always possible to find a repeating schedule of sub-exponential length.{{r|hrtv}}

With a compact input representation that specifies, for each distinct repeat time, the number of objects that have that repeat time, pinwheel scheduling is NP-hard.{{r|hrtv}}

Applications

Applications of pinwheel scheduling include scheduling communications between satellites and a ground station, scheduling maintenance of a collection of objects (such as oil changes for automobiles), computer processing of multimedia data,{{r|ll}} and contention resolution in real-time wireless computer networks.{{r|wsw}}

References

1. ^{{citation | last1 = Fishburn | first1 = P. C. | author1-link = Peter C. Fishburn | last2 = Lagarias | first2 = J. C. | author2-link = Jeffrey Lagarias | doi = 10.1007/s00453-002-0938-9 | issue = 1 | journal = Algorithmica | mr = 1912925 | pages = 14–38 | title = Pinwheel scheduling: achievable densities | volume = 34 | year = 2002}}
2. ^{{citation | last1 = Holte | first1 = Robert | last2 = Mok | first2 = Al | last3 = Rosier | first3 = Louis | last4 = Tulchinsky | first4 = Igor | last5 = Varvel | first5 = Donald | contribution = The pinwheel: a real-time scheduling problem | doi = 10.1109/hicss.1989.48075 | pages = 693–702 | publisher = IEEE Computer Society Press | title = Proceedings of the Twenty-Second Annual Hawaii International Conference on System Sciences, Volume II: Software Track | year = 1989}}
3. ^{{citation | last1 = Holte | first1 = Robert | last2 = Rosier | first2 = Louis | last3 = Tulchinsky | first3 = Igor | last4 = Varvel | first4 = Donald | doi = 10.1016/0304-3975(92)90365-M | issue = 1 | journal = Theoretical Computer Science | mr = 1171436 | pages = 105–135 | title = Pinwheel scheduling with two distinct numbers | volume = 100 | year = 1992}}. Previously announced at MFCS 1989.
4. ^{{citation | last1 = Lin | first1 = Shun-Shii | last2 = Lin | first2 = Kwei-Jay | doi = 10.1007/PL00009181 | issue = 4 | journal = Algorithmica | mr = 1470043 | pages = 411–426 | title = A pinwheel scheduler for three distinct numbers with a tight schedulability bound | volume = 19 | year = 1997}}
5. ^{{citation | last1 = Wu | first1 = Jean-Lien C. | last2 = Shin | first2 = Haw-Yun | last3 = Wu | first3 = Yi-Hsien | date = June 2005 | doi = 10.1080/02533839.2005.9671037 | issue = 4 | journal = Journal of the Chinese Institute of Engineers | pages = 701–711 | title = A pinwheel packet scheduling scheme for broadband wireless networks | volume = 28}}

Definition

Density

Periodicity and complexity

Applications

References

External links