- Definition
- Completeness
- Existence
- Application to the Berman–Hartmanis conjecture
- References
In computational complexity theory, polynomial creativity is a theory analogous to the theory of creative sets in recursion theory and mathematical logic. The {{mvar|k}}-creative sets are a family of formal languages in the complexity class NP whose complements certifiably do not have 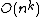 -time nondeterministic recognition algorithms.
-time nondeterministic recognition algorithms.
The {{mvar|k}}-creative sets are conjectured to form counterexamples to the Berman–Hartmanis conjecture on isomorphism of NP-complete sets. It is NP-complete to test whether an input string belongs to any one of these languages, but no polynomial time isomorphisms between all such languages and other NP-complete languages are known. Polynomial creativity and the {{mvar|k}}-creative sets were introduced in 1985 by Deborah Joseph and Paul Young, following earlier attempts to define polynomial analogues for creative sets by Ko and Moore.{{r|jy|km}}
Definition
Joseph and Young define the set 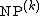 to be the set of nondeterministic Turing machine programs
to be the set of nondeterministic Turing machine programs  that, for inputs
that, for inputs  that they accept, have an accepting path with a number of steps that is at most
that they accept, have an accepting path with a number of steps that is at most 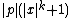 . This notation should be distinguished with that for the complexity class NP. The complexity class NP is a set of formal languages, while
. This notation should be distinguished with that for the complexity class NP. The complexity class NP is a set of formal languages, while 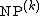 is instead a set of programs that accept some of these languages. Every language in NP is recognized by a program in one of the sets
is instead a set of programs that accept some of these languages. Every language in NP is recognized by a program in one of the sets 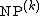 ; the parameter
; the parameter  is (up to the factor
is (up to the factor 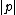 in the bound on the number of steps) the exponent in the polynomial running time of the program.{{r|jy}}
in the bound on the number of steps) the exponent in the polynomial running time of the program.{{r|jy}}
According to Joseph and Young's theory, a language  in NP is {{mvar|k}}-creative if it is possible to find a witness showing that the complement of
in NP is {{mvar|k}}-creative if it is possible to find a witness showing that the complement of  is not recognized by any program in
is not recognized by any program in 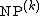 .
.
More formally, there should exist a polynomially computable function  that, when given a
that, when given a
nondeterministic program  in
in 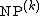 , finds an input
, finds an input 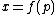 that either belongs to
that either belongs to  and causes the program to accept
and causes the program to accept  , or does not belong to
, or does not belong to  and causes the program to reject
and causes the program to reject  . The function
. The function  is called a productive function for
is called a productive function for  . If this productive function exists, the given program does not produce the behavior on input
. If this productive function exists, the given program does not produce the behavior on input  that would be expected of a program for recognizing the complement of
that would be expected of a program for recognizing the complement of  .{{r|jy}}
.{{r|jy}}
Completeness
Every  -creative set is NP-complete. For, applying a padding argument, there exists a polynomial-time translation
-creative set is NP-complete. For, applying a padding argument, there exists a polynomial-time translation  of the instances of any other language in NP into nondeterministic polynomial-time programs in
of the instances of any other language in NP into nondeterministic polynomial-time programs in 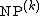 , such that yes-instances are translated into programs that accept all inputs and no-instances are translated into programs that reject all inputs. The composition of this translation with the function
, such that yes-instances are translated into programs that accept all inputs and no-instances are translated into programs that reject all inputs. The composition of this translation with the function  is a polynomial-time many-one reduction from the given language to the
is a polynomial-time many-one reduction from the given language to the  -creative set. It is also possible to prove more strongly that there exists an invertible parsimonious reduction to the
-creative set. It is also possible to prove more strongly that there exists an invertible parsimonious reduction to the  -creative set.{{r|jy}}
-creative set.{{r|jy}}
Existence
Joseph and Young define a polynomial-time function  to be polynomially honest if its running time is at most a polynomial function of its output length.
to be polynomially honest if its running time is at most a polynomial function of its output length.
This disallows, for instance, functions that take polynomial time but produce outputs of less than polynomial length. As they show, every one-to-one polynomially-honest function  is the productive function for a
is the productive function for a  -creative language
-creative language 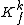 .{{r|jy}}
.{{r|jy}}
Given  , Joseph and Young define
, Joseph and Young define 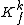 to be the set of values
to be the set of values 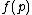 for nondeterministic programs
for nondeterministic programs  that have an accepting path for
that have an accepting path for 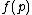 using at most
using at most 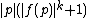 steps. This number of steps (on that input) would be consistent with
steps. This number of steps (on that input) would be consistent with  belonging to
belonging to 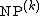 .
.
Then 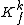 belongs to NP, for given an input
belongs to NP, for given an input 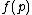 one can nondeterministically guess both
one can nondeterministically guess both  and its accepting path, and then verify that the path is valid for
and its accepting path, and then verify that the path is valid for  .{{r|jy}}
.{{r|jy}}
Language 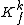 is
is  -creative, with
-creative, with  as its productive function, because every program
as its productive function, because every program  in
in 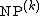 is mapped by
is mapped by  to a value
to a value 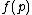 that is either accepted by
that is either accepted by  (and therefore also belongs to
(and therefore also belongs to 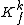 ) or rejected by
) or rejected by  (and therefore also does not belong to
(and therefore also does not belong to 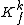 ).{{r|jy}}
).{{r|jy}}
Application to the Berman–Hartmanis conjecture
The Berman–Hartmanis conjecture states that there exists a polynomial-time isomorphism between any two NP-complete sets: a function that maps yes-instances of one such set one-to-one into yes-instances of the other, takes polynomial time, and whose inverse function can also be computed in polynomial time. It was formulated by Leonard C. Berman and Juris Hartmanis in 1977, based on the observation that all NP-complete sets known at that time were isomorphic.
An equivalent formulation of the conjecture is that every NP-complete set is paddable. This means that there exists a polynomial-time and polynomial-time-invertible one-to-one transformation 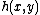 from yes-instances
from yes-instances  to larger yes-instances that encode the "irrelevant" information
to larger yes-instances that encode the "irrelevant" information  .{{r|bh}}
.{{r|bh}}
However, it is unknown how to find such a padding transformation for a  -creative language whose productive function is not polynomial-time-invertible. Therefore, if one-way permutations exist, the
-creative language whose productive function is not polynomial-time-invertible. Therefore, if one-way permutations exist, the  -creative languages having these permutations as their productive functions provide candidate counterexamples to the Berman–Hartmanis conjecture.{{r|jy}}
-creative languages having these permutations as their productive functions provide candidate counterexamples to the Berman–Hartmanis conjecture.{{r|jy}}
The (unproven) Joseph–Young conjecture formalizes this reasoning. The conjecture states that there exists a one-way length-increasing function  such that
such that 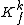 is not paddable.{{r|jy}} Alan Selman observed that this would imply a simpler conjecture, the encrypted complete set conjecture: there exists a one-way function
is not paddable.{{r|jy}} Alan Selman observed that this would imply a simpler conjecture, the encrypted complete set conjecture: there exists a one-way function  such that
such that 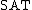 (the set of yes-instances for the satisfiability problem) and
(the set of yes-instances for the satisfiability problem) and 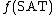 are non-isomorphic.{{r|s}}
are non-isomorphic.{{r|s}}
There exists an oracle relative to which one-way functions exist, both of these conjectures are false, and the Berman–Hartmanis conjecture is true.{{r|r}}
References
2. ^{{citation | last1 = Ko | first1 = Ker-I | last2 = Moore | first2 = Daniel | doi = 10.1137/0210061 | issue = 4 | journal = SIAM Journal on Computing | mr = 635436 | pages = 787–796 | title = Completeness, approximation and density | volume = 10 | year = 1981}}
3. ^{{citation | last = Rogers | first = John | doi = 10.1006/jcss.1997.1486 | issue = 3 | journal = Journal of Computer and System Sciences | mr = 1463764 | pages = 412–423 | title = The isomorphism conjecture holds and one-way functions exist relative to an oracle | volume = 54 | year = 1997}}
4. ^{{citation | last = Selman | first = Alan L. | doi = 10.1007/BF01374525 | issue = 3 | journal = Mathematical Systems Theory | mr = 1151339 | pages = 203–221 | title = A survey of one-way functions in complexity theory | volume = 25 | year = 1992}}
}}
- Constituency PP-61 (Faisalabad-XI)
- Constituency PP-62 (Faisalabad-XII)
- Constituency PP-63 (Faisalabad-XIII)
- Constituency PP-64 (Faisalabad-XIV)
- Constituency PP-65 (Faisalabad-XV)
- Constituency PP-66 (Faisalabad-XVI)
- Constituency PP-67 (Faisalabad-XVII)
- Constituency PP-67 (Mandi Bahauddin-III)
- Constituency PP-68 (Faisalabad-XVIII)
- Constituency PP-69 (Faisalabad-XIX)
- Constituency PP-70 (Faisalabad-XX)
- Constituency PP-71 (Faisalabad-XXI)
- Constituency PP-72 (Faisalabad-XXII)
- Constituency PP-73 (Jhang-I)
- Constituency PP-74 (Jhang-II)
- Constituency PP-75 (Jhang-III)
- Constituency PP-76 (Jhang-IV)
- Constituency PP-79 (Jhang-VII)
- Constituency PP-80 (Jhang-VIII)
- Constituency PP-81 (Jhang-IX)
- Constituency PP-82 (Jhang-X)
- Constituency PP-83 (Jhang-XI)
- Constituency PP-84 (Toba Tek Singh-I)
- Constituency PP-85 (Toba Tek Singh-II)
- Constituency PP-86 (Toba Tek Singh-III)