- Degree bound
- Algorithm
- Example
- References
In mathematics a P-recursive equation can be solved for polynomial solutions. Sergei A. Abramov in 1989 and Marko Petkovšek in 1992 described an algorithm which finds all polynomial solutions of those recurrence equations with polynomial coefficients.[1][2] The algorithm computes a degree bound for the solution in a first step. In a second step an ansatz for a polynomial of this degree is used and the unknown coefficients are computed by a system of linear equations. This article describes this algorithm.
In 1995 Abramov, Bronstein and Petkovšek showed that the polynomial case can be solved more efficiently by considering power series solution of the recurrence equation in a specific power basis (i.e. not the ordinary basis 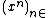 ).[3]
).[3]
Other algorithms which compute rational or hypergeometric solutions of a linear recurrence equation with polynomial coefficients also use algorithms which compute polynomial solutions.
Degree bound
Let  be a field of characteristic zero and
be a field of characteristic zero and 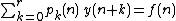 a recurrence equation of order
a recurrence equation of order  with polynomial coefficients
with polynomial coefficients 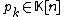 , polynomial right-hand side
, polynomial right-hand side 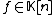 and unknown polynomial sequence
and unknown polynomial sequence 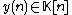 . Furthermore
. Furthermore  denotes the degree of a polynomial
denotes the degree of a polynomial 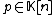 (with
(with 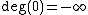 for the zero polynomial) and
for the zero polynomial) and 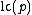 denotes the leading coefficient of the polynomial. Moreover let
denotes the leading coefficient of the polynomial. Moreover let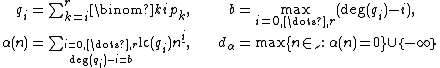 for
for 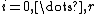 where
where 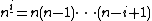 denotes the falling factorial and
denotes the falling factorial and  the set of nonegative integers. Then
the set of nonegative integers. Then  . This is called a degree bound for the polynomial solution
. This is called a degree bound for the polynomial solution  . This bound was shown by Abramov and Petkovšek.[1][2][3][4]
. This bound was shown by Abramov and Petkovšek.[1][2][3][4]
Algorithm
The algorithm consists of two steps. In a first step the degree bound is computed. In a second step an ansatz with a polynomial  of that degree with arbitrary coefficients in
of that degree with arbitrary coefficients in  is made and plugged into the recurrence equation. Then the different powers are compared and a system of linear equations for the coefficients of
is made and plugged into the recurrence equation. Then the different powers are compared and a system of linear equations for the coefficients of  is set up and solved. This is called the method undetermined coefficients.[5] The algorithm returns the general polynomial solution of a recurrence equation.
is set up and solved. This is called the method undetermined coefficients.[5] The algorithm returns the general polynomial solution of a recurrence equation.
'''algorithm''' polynomial_solutions '''is''' '''input:''' Linear recurrence equation. '''output:''' The general polynomial solution
if there are any solutions, otherwise false. '''for'''
'''do'''


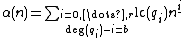
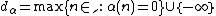
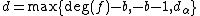
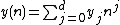 with unknown coefficients
with unknown coefficients  for
for 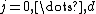
Compare coefficients of polynomialsand
to get possible values for
'''if''' there are possible values for
'''then''' '''return''' general solution
'''else''' '''return''' false '''end if'''
Example
Applying the formula for the degree bound on the recurrence equation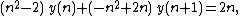 over
over  yields
yields  . Hence one can use an ansatz with a quadratic polynomial
. Hence one can use an ansatz with a quadratic polynomial  with
with 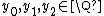 . Plugging this ansatz into the original recurrence equation leads to
. Plugging this ansatz into the original recurrence equation leads to This is equivalent to the following system of linear equations
This is equivalent to the following system of linear equations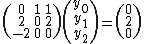 with the solution
with the solution 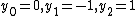 . Therefore the only polynomial solution is
. Therefore the only polynomial solution is  .
.
References
2. ^1 {{Cite journal|last=Petkovšek|first=Marko|date=1992|title=Hypergeometric solutions of linear recurrences with polynomial coefficients|journal=Journal of Symbolic Computation|volume=14|issue=2–3|pages=243–264|doi=10.1016/0747-7171(92)90038-6|issn=0747-7171}}
3. ^1 {{Cite book|last=Abramov|first=Sergei A.|last2=Bronstein|first2=Manuel|last3=Petkovšek|first3=Marko|date=1995|title=On polynomial solutions of linear operator equations|url=http://dl.acm.org/citation.cfm?id=220346.220384|journal=ISSAC '95 Proceedings of the 1995 International Symposium on Symbolic and Algebraic Computation|publisher=ACM|volume=|pages=290–296|doi=10.1145/220346.220384|isbn=978-0897916998|via=|citeseerx=10.1.1.46.9373}}
4. ^Weixlbaumer, Christian (2001). [https://www.risc.jku.at/research/combinat/software/DiffTools/pub/weixlbaumer01.pdf Solutions of difference equations with polynomial coefficients]. Diploma Thesis, Johannes Kepler Universität Linz
5. ^{{Cite book|url=https://www.math.upenn.edu/~wilf/Downld.html|title=A=B|last=Petkovšek|first=Marko|last2=Wilf|first2=Herbert S.|last3=Zeilberger|first3=Doron|date=1996|publisher=A K Peters|others=|isbn=978-1568810638|location=|pages=|oclc=33898705}}
- Tauroceras spadicigerum
- Taurocholate
- Tauroctony
- Taurodontism
- Tauro F.C.
- Taurogi
- Taurokathapsia
- Tauromaquia
- Tauron
- Tauron (Battlestar Galactica)
- Tauropine dehydrogenase
- Tauroscythians
- Taurotragus
- Taurpis Tula
- Taurunum
- Taurus 1
- Taurus 100
- Taurus 101
- Taurus 2
- Taurus 24/7
- Taurus 3
- Taurus 92
- Taurus 99
- Taurus Aldebaran
- Taurus (car)