- Formal definition
- General results Killing time Existence of a quasi-stationary distribution
- History
- Examples
- References
In probability a quasi-stationary distribution is a random process that admits one or several absorbing states that are reached almost surely, but is initially distributed such that it can evolve for a long time without reaching it. The most common example is the evolution of a population: the only equilibrium is when there is no one left, but if we model the number of people it is likely to remain stable for a long period of time before it eventually collapses.
Formal definition
We consider a Markov process 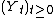 taking values in
taking values in 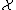 . There is a measurable set
. There is a measurable set 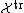 of absorbing states and
of absorbing states and  . We denote by
. We denote by 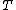 the hitting time of
the hitting time of 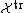 , also called killing time. We denote by
, also called killing time. We denote by 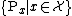 the family of distributions where
the family of distributions where 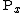 has original condition
has original condition 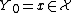 . We assume that
. We assume that 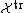 is almost surely reached, i.e.
is almost surely reached, i.e. 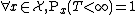 .
.
The general definition [1] is: a probability measure  on
on  is said to be a quasi-stationary distribution (QSD) if for every measurable set
is said to be a quasi-stationary distribution (QSD) if for every measurable set  contained in
contained in  ,
,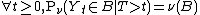 where
where  .
.
In particular 
General results
Killing time
From the assumptions above we know that the killing time is finite with probability 1. A stronger result than we can derive is that the killing time is exponentially distributed:[1][2] if  is a QSD then there exists
is a QSD then there exists  such that
such that 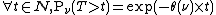 .
.
Moreover, for any 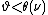 we get
we get 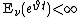 .
.
Existence of a quasi-stationary distribution
Most of the time the question asked is whether a QSD exists or not in a given framework. From the previous results we can derive a condition necessary to this existence.
Let 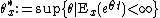 . A necessary condition for the existence of a QSD is
. A necessary condition for the existence of a QSD is  and we have the equality
and we have the equality 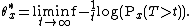
Moreover, from the previous paragraph, if  is a QSD then
is a QSD then 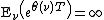 . As a consequence, if
. As a consequence, if  satisfies
satisfies 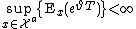 then there can be no QSD
then there can be no QSD  such that
such that 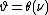 because other wise this would lead to the contradiction
because other wise this would lead to the contradiction 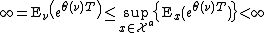 .
.
A sufficient condition for a QSD to exist is given considering the transition semigroup 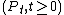 of the process before killing. Then, under the conditions that
of the process before killing. Then, under the conditions that  is a compact Hausdorff space and that
is a compact Hausdorff space and that  preserves the set of continuous functions, i.e.
preserves the set of continuous functions, i.e.  , there exists a QSD.
, there exists a QSD.
History
The works of Wright.[3] on gene frequency in 1931 and Yaglom[4] on branching processes in 1947 included already the idea of such distributions. The term quasi-stationarity applied to biological systems was then used by Barlett[5] in 1957, who later coined "quasi-stationary distribution" in.[6]
Quasi-stationary distributions were also part of the classification of killed processes given by Vere-Jones[7] in 1962 and their definition for finite state Markov chains was done in 1965 by Darroch and Seneta[8]
Examples
Quasi-stationary distributions can be used to model the following processes:
- Evolution of a population by the number of people: the only equilibrium is when there is no one left.
- Evolution of a contagious disease in a population by the number of people ill: the only equilibrium is when the disease disappears.
- Transmission of a gene: in case of several competing alleles we measure the number of people who have one and the absorbing state is when everybody has the same.
- Voter model: where everyone influences a small set of neighbors and opinions propagate, we study how many people vote for a particular party and an equilibrium is reached only when the party has no voter, or the whole population voting for it.
References
2. ^{{cite journal|jstor=1427713|title=Existence of Non-Trivial Quasi-Stationary Distributions in the Birth-Death Chain on JSTOR|journal=Advances in Applied Probability|volume=24|issue=4|pages=795–813|language=en|last1=Ferrari|first1=Pablo A.|last2=Martínez|first2=Servet|last3=Picco|first3=Pierre|year=1992}}
3. ^WRIGHT, Sewall. Evolution in Mendelian populations. Genetics, 1931, vol. 16, no 2, pp. 97–159.
4. ^YAGLOM, Akiva M. Certain limit theorems of the theory of branching random processes. In : Doklady Akad. Nauk SSSR (NS). 1947. p. 3.
5. ^BARTLETT, Mi S. On theoretical models for competitive and predatory biological systems. Biometrika, 1957, vol. 44, no 1/2, pp. 27–42.
6. ^BARTLETT, Maurice Stevenson. Stochastic population models; in ecology and epidemiology. 1960.
7. ^{{Cite journal|last=VERE-JONES|first=D.|date=1962-01-01|title=GEOMETRIC ERGODICITY IN DENUMERABLE MARKOV CHAINS|journal=The Quarterly Journal of Mathematics|language=en|volume=13|issue=1|pages=7–28|doi=10.1093/qmath/13.1.7|issn=0033-5606}}
8. ^{{Cite journal|last=Darroch|first=J. N.|last2=Seneta|first2=E.|date=1965|title=On Quasi-Stationary Distributions in Absorbing Discrete-Time Finite Markov Chains|jstor=3211876|journal=Journal of Applied Probability|volume=2|issue=1|pages=88–100|doi=10.2307/3211876}}
- 2011-12 GNK Dinamo Zagreb season
- 2011-12 Gold Coast United season
- 2011-12 Golden State Warriors season
- 2011-12 Gonzaga Bulldogs men's basketball team
- 2011-12 Granada CF season
- 2011-12 Great American Conference Championships
- 2011-12 Greek Football Cup
- 2011-12 Green Bay Phoenix men's basketball team
- 2011-12 Greenock Morton F.C. season
- 2011-12 Grimsby Town F.C. season
- 2011-12 Győri ETO FC season
- 2011-12 Hamilton Academical F.C. season
- 2011-12 Hannover 96 season
- 2011-12 Hapoel Tel Aviv F.C. season
- 2011-12 Hartlepool United F.C. season
- 2011-12 Harvard Crimson men's basketball team
- 2011-12 Harvard Crimson women's ice hockey season
- 2011-12 Hazfi Cup
- 2011-12 HB Køge season
- 2011-12 Heart of Midlothian F.C. season
- 2011-12 Heineken Cup
- 2011-12 heineken cup
- 2011-12 Heineken Cup pool stage
- 2011-12 Hereford United F.C. season
- 2011-12 Hertha Berlin season