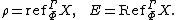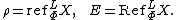- Definition
- Examples
- See also
- Notes
- References
In category theory and related fields of mathematics, a refinement is a construction that generalizes the operations of "interior enrichment", like bornologification or saturation of a locally convex space. A dual construction is called envelope.
Definition
Suppose  is a category,
is a category,  an object in
an object in  , and
, and  and
and  two classes of morphisms in
two classes of morphisms in  . The definition{{sfn|Akbarov|2016|p=52}} of a refinement of
. The definition{{sfn|Akbarov|2016|p=52}} of a refinement of  in the class
in the class  by means of the class
by means of the class  consists of two steps.
consists of two steps.
- A morphism
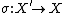 in
in  is called an enrichment of the object
is called an enrichment of the object  in the class of morphisms
in the class of morphisms  by means of the class of morphisms
by means of the class of morphisms  , if
, if 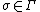 , and for any morphism
, and for any morphism 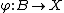 from the class
from the class  there exists a unique morphism
there exists a unique morphism 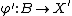 in
in  such that
such that  .
.
- An enrichment
 of the object
of the object  in the class of morphisms
in the class of morphisms  by means of the class of morphisms
by means of the class of morphisms  is called a refinement of
is called a refinement of  in
in  by means of
by means of  , if for any other enrichment
, if for any other enrichment 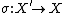 (of
(of  in
in  by means of
by means of  ) there is a unique morphism
) there is a unique morphism  in
in  such that
such that 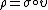 . The object
. The object  is also called a refinement of
is also called a refinement of  in
in  by means of
by means of  .
.
Notations:
In a special case when  is a class of all morphisms whose ranges belong to a given class of objects
is a class of all morphisms whose ranges belong to a given class of objects  in
in  it is convenient to replace
it is convenient to replace  with
with  in the notations (and in the terms):
in the notations (and in the terms):
Similarly, if  is a class of all morphisms whose ranges belong to a given class of objects
is a class of all morphisms whose ranges belong to a given class of objects  in
in  it is convenient to replace
it is convenient to replace  with
with  in the notations (and in the terms):
in the notations (and in the terms):
For example, one can speak about a refinement of  in the class of objects
in the class of objects  by means of the class of objects
by means of the class of objects  :
:
Examples
- The bornologification{{sfn|Kriegl|Michor|1997|p=35}}{{sfn|Akbarov|2016|p=57}}
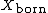 of a locally convex space
of a locally convex space  is a refinement of
is a refinement of  in the category
in the category 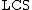 of locally convex spaces by means of the subcategory
of locally convex spaces by means of the subcategory 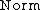 of normed spaces:
of normed spaces: 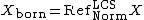
- The saturation{{sfn|Akbarov|2003|p=194}}{{sfn|Akbarov|2016|p=57}}
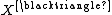 of a pseudocomplete&91;1&93; locally convex space
of a pseudocomplete&91;1&93; locally convex space  is a refinement in the category
is a refinement in the category 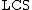 of locally convex spaces by means of the subcategory
of locally convex spaces by means of the subcategory 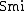 of the Smith spaces:
of the Smith spaces: 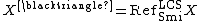
See also
- Envelope
Notes
 is said to be pseudocomplete if each totally bounded Cauchy net in
is said to be pseudocomplete if each totally bounded Cauchy net in  converges.
converges.References
- {{cite book |last=Kriegl |first=A. | last2=Michor |first2=P.W. |date= 1997 |title= The convenient setting of global analysis |url= https://bookstore.ams.org/surv-53 |location= Providence, Rhode Island |publisher= American Mathematical Society |isbn=0-8218-0780-3| ref = harv}}
- {{cite journal|last=Akbarov|first=S.S.|title=Pontryagin duality in the theory of topological vector spaces and in topological algebra|journal=Journal of Mathematical Sciences|year=2003|volume=113|issue=2|pages=179–349|doi=10.1023/A:1020929201133|url=http://www.springerlink.com/content/k62m72960101g6q2/| ref = harv}}
- {{cite journal|last=Akbarov|first=S.S.|title=Envelopes and refinements in categories, with applications to functional analysis|url=https://www.impan.pl/en/publishing-house/journals-and-series/dissertationes-mathematicae/all/513|journal=Dissertationes Mathematicae|year=2016|volume=513|pages=1–188|arxiv=1110.2013|doi=10.4064/dm702-12-2015| ref = harv}}
- La Chapelle-aux-Chasses
- La Chapelle-aux-Choux
- La Chapelle-aux-Filtzmeens
- La Chapelle-aux-Filtzméens
- La Chapelle-aux-Lys
- La Chapelle-aux-Naux
- Lachapelle-aux-Pots
- La Chapelle-aux-Saints
- La Chapelle-aux Saints 1
- Lachapelle-Auzac
- La Chapelle-Baloue
- La Chapelle-Basse-Mer
- La Chapelle-Baton
- La Chapelle-Baton, Deux-Sevres
- La Chapelle-Baton, Vienne
- La Chapelle-Bayvel
- La Chapelle-Bertin
- La Chapelle-Bertrand
- La Chapelle-Biche
- La Chapelle Blanche
- La Chapelle-Blanche
- La Chapelle-Blanche, Cotes-d'Armor
- La Chapelle-Blanche, Côtes-d'Armor
- La Chapelle-Blanche-Saint-Martin
- La Chapelle-Blanche, Savoie