“Regular distribution (economics)”的意思、由来-开放百科全书

Distributions that satisfy the regularity condition are often referred to as "regular distributions".

Definitions

Both are defined for continuous distributions, although analogs for discrete distributions have also been considered.^[2]

Concavity of revenue in quantile space

Consider a seller auctioning a single item to a buyer with random value

. For any price

set by the seller, the buyer will buy the item if

. The seller's expected revenue is

. We define the revenue function

as follows:

In other words,

is the revenue that can be obtained by selling the item with (ex-ante) probability

Monotone virtual valuation

For a cumulative distribution function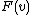

and corresponding probability density function

, the virtual valuation of the agent is defined as

The valuation distribution is said to be regular if

is monotone non-decreasing function.^[3]

Applications

Myerson's auction

An important special case^[4] considered by {{harvtxt|Myerson|1981}} is the problem of a seller auctioning a single item to one or more buyers whose valuations for the item are drawn from independent distributions.

Myerson showed that the problem of the seller truthfully maximizing her profit is equivalent to maximizing the "virtual social welfare", i.e. the expected virtual valuation of the bidder who receives the item.

When the bidders valuations distributions are regular, the virtual valuations are monotone in the real valuations, which implies that the transformation to virtual valuations is incentive compatible.

Thus a Vickrey auction can be used to maximize the virtual social welfare (with additional reserve prices to guarantee non-negative virtual valuations).

When the distributions are irregular, a more complicated ironing procedure is used to transform them into regular distributions.^[5]

Prior-independent mechanism design

Myerson's auction mentioned above is optimal if the seller has an accurate prior, i.e. a good estimate of the distribution of valuations that bidders can have for the item.

Prior-independent mechanism design seeks to design mechanisms for sellers (and agents in general) who do not have access to such a prior.

Regular distributions are a common assumption in prior-independent mechanism design.

For example, the seminal {{harvtxt|Bulow|Klemperer|1996}} proved that if bidders valuations for a single item are regular and i.i.d. (or identical and affiliated),

the revenue obtained from selling with an English auction to

bidders dominates the revenue obtained from selling with any mechanism (in particular, Myerson's optimal mechanism) to

bidders.

Notes

1. ^{{cite journal|doi = 10.1145/2728732.2728733|title = Approximately optimal mechanism design: motivation, examples, and lessons learned|journal = SIGecom Exchanges|volume = 13|number = 2|pages = 4–20|year = 2014|author = Tim Roughgarden|arxiv = 1406.6773}}
2. ^{{cite conference|ISBN = 978-0-898716-24-5|title = Designing and learning optimal finite support auctions|conference = SODA 2007|pages = 736–745|year = 2007|author = Edith Elkind| publisher = SIAM}}
3. ^¹{{cite book |last= Hartline|first= Jason |date= 2012|title= Mechanism Design and Approximation|url= http://jasonhartline.com/MDnA/|chapter = 3.3}}
4. ^Myerson distinguishes between "preference uncertainty", which we expect to be independent for each bidder, and "quality uncertainty", which is treated in a more general model where one bidder's private information affects the valuation of other bidders, and even the value of the item to the seller.
5. ^{{Cite journal | title = Optimal Auction Design | author = Roger Myerson| journal = Mathematics of Operations Research | volume = 6 | issue = 1 | pages = 58–73 | publisher = INFORMS | doi = 10.1287/moor.6.1.58 | date = February 1981 | url = https://doi.org/10.1287/moor.6.1.58 | ref = harv | postscript = .}}