- Textbooks
- References
- External links
Sir (Alfred) George Greenhill, F.R.S. (29 November 1847 in London – 10 February 1927 in London), was a British mathematician.
George Greenhill was educated at Christ's Hospital School and from there he went up to St John's College, Cambridge in 1866.[1] In 1876, Greenhill was appointed professor of mathematics at the Royal Military Academy (RMA) at Woolwich, London, UK.[2] He held this chair until his retirement in 1908. His 1892 textbook on applications of elliptic functions is of acknowledged excellence. He was one of the world's leading experts on applications of elliptic integrals in electromagnetic theory.[3] He was a Plenary Speaker of the ICM in 1904 at Heidelberg[4] and an Invited Speaker of the ICM in 1908 at Rome, in 1920 at Strasbourg,[5] and in 1924 at Toronto.
In 1879, Greenhill developed a rule of thumb for calculating the optimal twist rate for lead-core bullets. This shortcut uses the bullet's length, needing no allowances for weight or nose shape.[6] Greenhill applied this theory to account for the steadiness of flight conferred upon an elongated projectile by rifling. The eponymous Greenhill Formula, still used today, is:
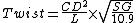
where:
- C = 150 (use 180 for muzzle velocities higher than 2,800 f/s)
- D = bullet's diameter in inches
- L = bullet's length in inches
- SG = bullet's specific gravity (10.9 for lead-core bullets, which cancels out the second half of the equation)
The original value of C was 150, which yields a twist rate in inches per turn, when given the diameter D and the length L of the bullet in inches. This works to velocities of about 840 m/s (2800 ft/s); above those velocities, a C of 180 should be used. For instance, with a velocity of 600 m/s (2000 ft/s), a diameter of {{convert|0.5|in|mm}} and a length of {{convert|1.5|in|mm}}, the Greenhill formula would give a value of 25, which means 1 turn in {{convert|25|in|mm}}.
Textbooks
- A. G. Greenhill Differential and integral calculus, with applications ( London, MacMillan, 1886) [https://archive.org/details/differentialinte00greeuoft archive.org]
- A. G. Greenhill, The applications of elliptic functions (MacMillan & Co, New York, 1892)[7] University of Michigan Historical Mathematical Collection
- A. G. Greenhill, A treatise on hydrostatics (MacMillan, London, 1894) [https://archive.org/details/treatiseonhydros00greeuoft archive.org]
- A. G. Greenhill, The dynamics of mechanical flight (Constable, London, 1912) [https://archive.org/details/dynamicsofmechan00greerich archive.org]
- A. G. Greenhill, [https://catalog.hathitrust.org/Record/008915822 Report on gyroscopic theory] (Darling & Son, 1914)[8]
References
2. ^{{MacTutor Biography|id=Greenhill}}
3. ^{{cite journal|author=Greenhill, Alfred George|title=The elliptic integral in electromagnetic theory|journal=Bull. Amer. Math. Soc.|year=1907|volume=8|pages=447–534|mr=1500798|doi=10.1090/s0002-9947-1907-1500798-2}}
4. ^{{cite book|chapter=The Mathematical Theory of the Top considered historically by A. G. Greenhill|pages=100–108|title=Verhandlungen des dritten Mathematiker-Kongresses in Heidelberg von 8. bis 13. August 1904|location=Leipzig|publisher=B. G. Teubner|year=1905|chapter-url=https://babel.hathitrust.org/cgi/pt?id=miun.aag4063.0004.001;view=1up;seq=114}}
5. ^{{cite book|chapter-url=http://www.mathunion.org/ICM/ICM1920/Main/icm1920.0636.0655.ocr.pdf|pages=636–655|year=1921|title=Compte rendu du Congrès international des mathématiciens tenu à Strasbourg du 22 au 30 Septembre 1920|chapter=The Fourier and Bessel Functions contrasted by G. Greenhill}}
6. ^Mosdell, Matthew. The Greenhill Formula. {{cite web|url=http://www.mamut.net/MarkBrooks/newsdet35.htm |title=Archived copy |accessdate=2009-08-19 |deadurl=yes |archiveurl=https://web.archive.org/web/20110718205935/http://www.mamut.net/MarkBrooks/newsdet35.htm |archivedate=2011-07-18 }} (Accessed 2009 AUG 19)
7. ^{{cite journal|author=Harkness, J.|authorlink=James Harkness|title=Review: The Applications of Elliptic Functions by Alfred George Greenhill|journal=Bull. Amer. Math. Soc.|year=1893|volume=2|issue=7|pages=151–157|url=http://www.ams.org/journals/bull/1893-02-07/S0002-9904-1893-00129-8/S0002-9904-1893-00129-8.pdf|doi=10.1090/s0002-9904-1893-00129-8}}
8. ^{{cite journal|author=Wilson, Edwin Bidwell|authorlink=Edwin Bidwell Wilson|title=Review: Report on Gyroscopic Theory by Sir G. Greenhill|journal=Bull. Amer. Math. Soc.|year=1917|volume=23|issue=5|pages=241–244|url=http://www.ams.org/journals/bull/1917-23-05/S0002-9904-1917-02930-8/S0002-9904-1917-02930-8.pdf|doi=10.1090/s0002-9904-1917-02930-8}}
External links
{{Wikisource author}}- {{wikiquote-inline}}
- Alfred George Greenhill. The First Century of the ICMI (1909 - 2008)
- Lopoczno
- Lopoen Tenzin Namdak
- Lopohan language
- Lopo Homem
- Lopoke
- Lopon
- Lopon Tenzin Namdak
- L'Opoponax
- Loporotomy
- Loporzano
- Loporzano, Huesca
- Loporzano, Spain
- Lopo Soares
- Lopou
- Lopo Vaz de Sampaio
- Lopovi prve klase
- Lopovi prve klase (2005)
- LOPP
- Lopp
- Loppem
- Loppenow
- Loppersum railway station
- Loppijarvi
- Loppijärvi
- Loppiner see