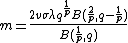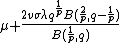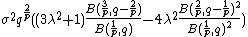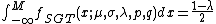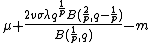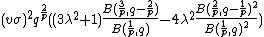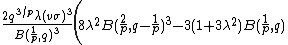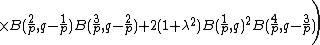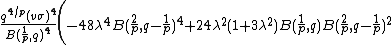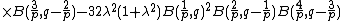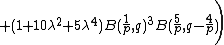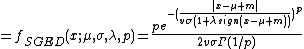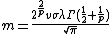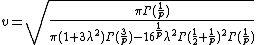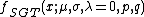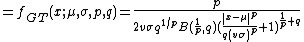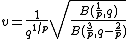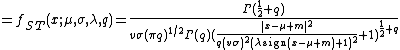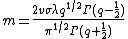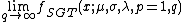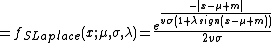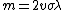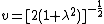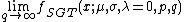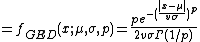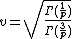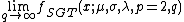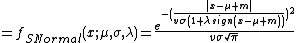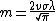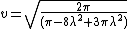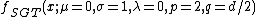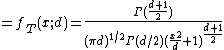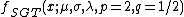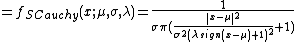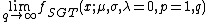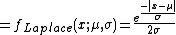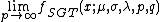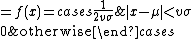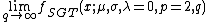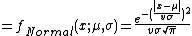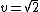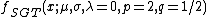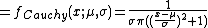- Definition Probability density function Moments
- Special Cases Skewed generalized error distribution Generalized t distribution Skewed t distribution Skewed Laplace distribution Generalized error distribution Skewed normal distribution Student's t-distribution Skewed Cauchy distribution Laplace distribution Uniform Distribution Normal distribution Cauchy Distribution
- References
- External links
- Notes
In probability and statistics, the skewed generalized “t” distribution is a family of continuous probability distributions. The distribution was first introduced by Panayiotis Theodossiou[1] in 1998. The distribution has since been used in different applications.[2][3][4][5][6][7] There are different parameterizations for the skewed generalized t distribution,[1][5] which we account for in this article.
Definition
Probability density function
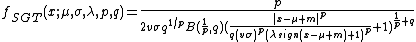
where  is the beta function,
is the beta function,  is the location parameter,
is the location parameter, 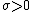 is the scale parameter,
is the scale parameter, 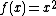 is the skewness parameter, and
is the skewness parameter, and 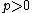 and
and 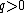 are the parameters that control the kurtosis. Note that
are the parameters that control the kurtosis. Note that  and
and  are not parameters, but functions of the other parameters that are used here to scale or shift the distribution appropriately to match the various parameterizations of this distribution.
are not parameters, but functions of the other parameters that are used here to scale or shift the distribution appropriately to match the various parameterizations of this distribution.
In the original parameterization[1] of the skewed generalized t distribution,
and
.
These values for  and
and  yield a distribution with mean of
yield a distribution with mean of  if
if 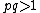 and a variance of
and a variance of  if
if 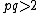 . In order for
. In order for  to take on this value however, it must be the case that
to take on this value however, it must be the case that 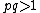 . Similarly, for
. Similarly, for  to equal the above value,
to equal the above value, 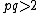 .
.
The parameterization that yields the simplest functional form of the probability density function sets  and
and 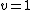 . This gives a mean of
. This gives a mean of
and a variance of
The  parameter controls the skewness of the distribution. To see this, let
parameter controls the skewness of the distribution. To see this, let  denote the mode of the distribution, and note that
denote the mode of the distribution, and note that
Since 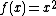 , the probability left of the mode, and therefore right of the mode as well, can equal any value in (0,1) depending on the value of
, the probability left of the mode, and therefore right of the mode as well, can equal any value in (0,1) depending on the value of  . Thus the skewed generalized t distribution can be highly skewed as well as symmetric. If
. Thus the skewed generalized t distribution can be highly skewed as well as symmetric. If 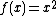 , then the distribution is negatively skewed. If
, then the distribution is negatively skewed. If 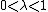 , then the distribution is positively skewed. If
, then the distribution is positively skewed. If  , then the distribution is symmetric.
, then the distribution is symmetric.
Finally,  and
and  control the kurtosis of the distribution. As
control the kurtosis of the distribution. As  and
and  get smaller, the kurtosis increases[1] (i.e. becomes more leptokurtic). Large values of
get smaller, the kurtosis increases[1] (i.e. becomes more leptokurtic). Large values of  and
and  yield a distribution that is more platykurtic.
yield a distribution that is more platykurtic.
Moments
Let  be a random variable distributed with the skewed generalized t distribution.The
be a random variable distributed with the skewed generalized t distribution.The 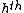 moment (i.e.
moment (i.e. 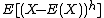 ), for
), for  , is:
, is:
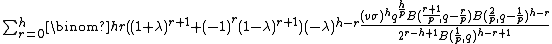
The mean, for 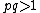 , is:
, is:
The variance (i.e. 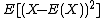 ), for
), for 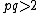 , is:
, is:
The skewness (i.e. 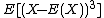 ), for
), for 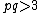 , is:
, is:
The kurtosis (i.e.  ), for
), for 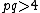 , is:
, is:
Special Cases
Special and limiting cases of the skewed generalized t distribution include the skewed generalized error distribution, the generalized t distribution introduced by McDonald and Newey,[6] the skewed t proposed by Hansen, the skewed Laplace distribution, the generalized error distribution (also known as the generalized normal distribution), a skewed normal distribution, the student t distribution, the skewed Cauchy distribution, the Laplace distribution, the uniform distribution, the normal distribution, and the Cauchy distribution. The graphic below, adapted from Hansen, McDonald, and Newey,[2] shows which parameters should be set to obtain some of the different special values of the skewed generalized t distribution.
Skewed generalized error distribution
The Skewed Generalized Error Distribution has the pdf:
where
gives a mean of  . Also
. Also
gives a variance of  .
.
Generalized t distribution
The Generalized T Distribution has the pdf:
where
gives a variance of  .
.
Skewed t distribution
The Skewed T Distribution has the pdf:
where
gives a mean of  . Also
. Also
gives a variance of  .
.
Skewed Laplace distribution
The Skewed Laplace Distribution has the pdf:
where
gives a mean of  . Also
. Also
gives a variance of  .
.
Generalized error distribution
The Generalized Error Distribution (also known as the generalized normal distribution) has the pdf:
where
gives a variance of  .
.
Skewed normal distribution
The Skewed Normal Distribution has the pdf:
where
gives a mean of  . Also
. Also
gives a variance of  .
.
Student's t-distribution
The Student's t-distribution has the pdf:
Note that we substituted 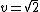 .
.
Skewed Cauchy distribution
The Skewed Cauchy Distribution has the pdf:
Note that we substituted 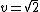 and
and  .
.
Also note that the mean, variance, skewness, and kurtosis of the skewed Cauchy distribution are all undefined.
Laplace distribution
The Laplace distribution has the pdf:
Note that we substituted 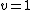 .
.
Uniform Distribution
The Uniform distribution has the pdf:
Thus the standard uniform parameterization is obtained if 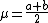 ,
, 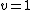 , and
, and 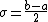 .
.
Normal distribution
The Normal distribution has the pdf:
where
gives a variance of  .
.
Cauchy Distribution
The Cauchy distribution has the pdf:
Note that we substituted 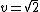 .
.
References
- {{Cite journal
| last1 = Hansen | first1 = B.
| year = 1994
| title = Autoregressive Conditional Density Estimation
| journal = International Economic Review
| volume = 35
| issue = 3
| pages = 705–730
| doi=10.2307/2527081
| jstor = 2527081
}}
- {{Cite journal
| last1 = Hansen | first1 = C.
| last2 = McDonald | first2 = J.
| last3 = Newey | first3 = W.
| year = 2010
| title = Instrumental Variables Estimation with Flexible Distributions
| journal = Journal of Business and Economic Statistics
| volume = 28
| pages = 13–25
| doi=10.1198/jbes.2009.06161
}}
- {{Cite journal
| last1 = Hansen | first1 = C.
| last2 = McDonald | first2 = J.
| last3 = Theodossiou | first3 = P.
| year = 2007
| title = Some Flexible Parametric Models for Partially Adaptive Estimators of Econometric Models
| journal = Economics: The Open-Access, Open-Assessment E-Journal
| volume = 1
| issue = 2007–7
| pages = 1
| doi = 10.5018/economics-ejournal.ja.2007-7
}}
- {{Cite journal
| last1 = McDonald | first1 = J.
| last2 = Michefelder | first2 = R.
| last3 = Theodossiou | first3 = P.
| year = 2009
| title = Evaluation of Robust Regression Estimation Methods and Intercept Bias: A Capital Asset Pricing Model Application
| journal = Multinational Finance Journal
| volume = 15
| issue = 3/4
| pages = 293–321
| doi = 10.17578/13-3/4-6
}}
- {{Cite journal
| last1 = McDonald | first1 = J.
| last2 = Michelfelder | first2 = R.
| last3 = Theodossiou | first3 = P.
| year = 2010
| title = Robust Estimation with Flexible Parametric Distributions: Estimation of Utility Stock Betas
| journal = Quantitative Finance
| volume = 10
| issue = 4
| pages = 375–387
| doi = 10.1080/14697680902814241
}}
- {{Cite journal
| last1 = McDonald | first1 = J.
| last2 = Newey | first2 = W.
| year = 1988
| title = Partially Adaptive Estimation of Regression Models via the Generalized t Distribution
| journal = Econometric Theory
| volume = 4
| issue = 3
| pages = 428–457
| doi=10.1017/s0266466600013384
}}
- {{Cite journal
| last1 = Savva | first1 = C.
| last2 = Theodossiou | first2 = P.
| year = 2015
| title = Skewness and the Relation between Risk and Return
|journal = Management Science
}}
- {{Cite journal
| last1 = Theodossiou | first1 = P.
| year = 1998
| title = Financial Data and the Skewed Generalized T Distribution
|journal = Management Science
| volume = 44
| issue = 12–part–1
| pages = 1650–1661
| doi=10.1287/mnsc.44.12.1650
}}
External links
- [https://cran.r-project.org/web/packages/sgt/vignettes/sgt.pdf outlines skewed generalized t distribution, its special cases, and a program to calculate its pdf, cdf, and critical values]
Notes
2. ^1 Hansen, C., J. McDonald, and P. Theodossiou (2007) "Some Flexible Parametric Models for Partially Adaptive Estimators of Econometric Models" Economics: The Open-Access, Open-Assessment E-Journal
3. ^1 {{cite journal | last1 = McDonald | first1 = J. | last2 = Michelfelder | first2 = R. | last3 = Theodossiou | first3 = P. | year = 2009 | title = Evaluation of Robust Regression Estimation Methods and Intercept Bias: A Capital Asset Pricing Model Application | url = | journal = Multinational Finance Journal | volume = 15 | issue = 3/4| pages = 293–321 | doi = 10.17578/13-3/4-6 }}
4. ^1 2 McDonald J., R. Michelfelder, and P. Theodossiou (2010) "Robust Estimation with Flexible Parametric Distributions: Estimation of Utility Stock Betas" Quantitative Finance 375-387.
5. ^1 2 {{cite journal | last1 = McDonald | first1 = J. | last2 = Newey | first2 = W. | year = 1998 | title = Partially Adaptive Estimation of Regression Models via the Generalized t Distribution | url = | journal = Econometric Theory | volume = 4 | issue = 3| pages = 428–457 | doi = 10.1017/S0266466600013384 }}
6. ^1 Savva C. and P. Theodossiou (2015) "Skewness and the Relation between Risk and Return" Management Science, forthcoming.
7. ^1 2 3 4 {{cite journal | last1 = Theodossiou | first1 = P | year = 1998 | title = Financial Data and the Skewed Generalized T Distribution | url = | journal = Management Science | volume = 44 | issue = 12–part–1| pages = 1650–1661 | doi=10.1287/mnsc.44.12.1650}}
- [1]
- [2]
- [3]
- [4]
- [5]
- [6]
- [7]
}}{{ProbDistributions|continuous-infinite}}{{Statistics|state=collapsed}}{{DEFAULTSORT:Skewed generalized t distribution}}
- Gabriela Mosqueira Benitez
- Gabriela Mosqueira Benítez
- Gabriela Mosquera
- Gabriela N
- Gabriela N.
- Gabriela (name)
- Gabriela Navrátilová
- Gabriel Andreas Stoud Platou
- Gabriel and Sarah Stacy
- Gabriela Niculescu
- Gabriela Nikitina
- Gabriel Antoine Obertan
- Gabriela Nunez
- Gabriela Ordoñez
- Gabriela Ortiz Martínez
- Gabriela Paz-Franco
- Gabriela Pena
- Gabriela Perianu
- Gabriela Petrova
- Gabriela Pichler
- Gabriela Pizarro
- Gabriela Pochinki
- Gabriela pochinki
- Gabriel Appelt Pires
- Gabriela Pulgar