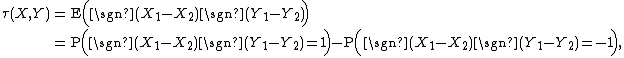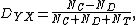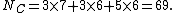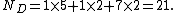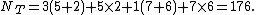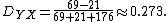- Somers’ D for sample
- Somers’ D for distribution
- Somers' D for binary dependent variables Example
- References
In statistics, Somers’ D, sometimes incorrectly referred to as Somer’s D, is a measure of ordinal association between two possibly dependent random variables {{mvar|X}} and {{mvar|Y}}. Somers’ D takes values between  when all pairs of the variables disagree and
when all pairs of the variables disagree and  when all pairs of the variables agree. Somers’ D is named after Robert H. Somers, who proposed it in 1962.[1]
when all pairs of the variables agree. Somers’ D is named after Robert H. Somers, who proposed it in 1962.[1]
Somers’ D plays a central role in rank statistics and is the parameter behind many nonparametric methods.[2] It is also used as a quality measure of binary choice or ordinal regression (e.g., logistic regressions) and credit scoring models.
Somers’ D for sample
We say that two pairs  and
and 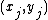 are concordant if the ranks of both elements agree, or
are concordant if the ranks of both elements agree, or 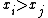 and
and 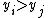 or if
or if 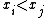 and
and 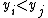 . We say that two pairs
. We say that two pairs  and
and 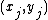 are discordant, if the ranks of both elements disagree, or if
are discordant, if the ranks of both elements disagree, or if 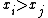 and
and 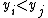 or if
or if 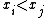 and
and 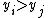 . If
. If 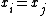 or
or 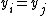 , the pair is neither concordant nor discordant.
, the pair is neither concordant nor discordant.
Let 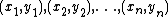 be a set of observations of two possibly dependent random vectors {{mvar|X}} and {{mvar|Y}}. Define Kendall tau rank correlation coefficient
be a set of observations of two possibly dependent random vectors {{mvar|X}} and {{mvar|Y}}. Define Kendall tau rank correlation coefficient  as
as
where 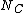 is the number of concordant pairs and
is the number of concordant pairs and  is the number of discordant pairs. Somers’ D of {{mvar|Y}} with respect to {{mvar|X}} is defined as
is the number of discordant pairs. Somers’ D of {{mvar|Y}} with respect to {{mvar|X}} is defined as 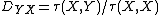 .[2] Note that Kendall's tau is symmetric in {{mvar|X}} and {{mvar|Y}}, whereas Somers’ D is asymmetric in {{mvar|X}} and {{mvar|Y}}.
.[2] Note that Kendall's tau is symmetric in {{mvar|X}} and {{mvar|Y}}, whereas Somers’ D is asymmetric in {{mvar|X}} and {{mvar|Y}}.
As 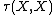 quantifies the number of pairs with unequal {{mvar|X}} values, Somers’ D is the difference between the number of concordant and discordant pairs, divided by the number of pairs with {{mvar|X}} values in the pair being unequal.
quantifies the number of pairs with unequal {{mvar|X}} values, Somers’ D is the difference between the number of concordant and discordant pairs, divided by the number of pairs with {{mvar|X}} values in the pair being unequal.
Somers’ D for distribution
Let two independent bivariate random variables 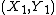 and
and  have the same probability distribution
have the same probability distribution 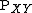 . Again, Somers’ D, which measures ordinal association of random variables {{mvar|X}} and {{mvar|Y}} in
. Again, Somers’ D, which measures ordinal association of random variables {{mvar|X}} and {{mvar|Y}} in 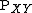 , can be defined through Kendall's tau
, can be defined through Kendall's tau
or the difference between the probabilities of concordance and discordance. Somers’ D of {{mvar|Y}} with respect to {{mvar|X}} is defined as 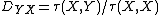 . Thus,
. Thus, 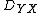 is the difference between the two corresponding probabilities, conditional on the {{mvar|X}} values not being equal.
is the difference between the two corresponding probabilities, conditional on the {{mvar|X}} values not being equal.
If {{mvar|X}} has a continuous probability distribution, then 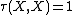 and Kendall's tau and Somers’ D coincide. Somers’ D normalizes Kendall's tau for possible mass points of variable {{mvar|X}}.
and Kendall's tau and Somers’ D coincide. Somers’ D normalizes Kendall's tau for possible mass points of variable {{mvar|X}}.
If {{mvar|X}} and {{mvar|Y}} are both binary with values 0 and 1, then Somers’ D is the difference between two probabilities:
Somers' D for binary dependent variables
In practice, Somers' D is most often used when the dependent variable Y is a binary variable,[2] i.e. for binary classification or prediction of binary outcomes including binary choice models in econometrics. Methods for fitting such models include logistic and probit regression.
Several statistics can be used to quantify the quality of such models: area under the receiver operating characteristic (ROC) curve, Goodman and Kruskal's gamma, Kendall's tau (Tau-a), Somers’ D, etc. Somers’ D is probably the most widely used of the available ordinal association statistics.[3] If there are no ties on independent variable, Somers’ D is related to the area under the receiver operating characteristic curve (AUC),
.
In the case where the independent (predictor) variable {{mvar|X}} is {{em|discrete}} and the dependent (outcome) variable {{mvar|Y}} is binary, Somers’ D equals
where 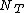 is the number of neither concordant nor discordant pairs that are tied on variable {{mvar|Y}} and not on variable {{mvar|X}}.
is the number of neither concordant nor discordant pairs that are tied on variable {{mvar|Y}} and not on variable {{mvar|X}}.
Example
Suppose that the independent (predictor) variable {{mvar|X}} takes three values, {{val|0.25}}, {{val|0.5}}, or {{val|0.75}}, and dependent (outcome) variable {{mvar|Y}} takes two values, {{val|0}} or {{val|1}}. The table below contains observed combinations of {{mvar|X}} and {{mvar|Y}}:
| {{mvar|Y|{{mvar|X | 0.25 | 0.5 | 0.75 |
|---|---|---|---|
| 0 | 3}} | 5}} | 2}} |
| 1 | 1}} | 7}} | 6}} |
The number of concordant pairs equals
The number of discordant pairs equals
The number of pairs tied on {{mvar|Y}} but not on {{mvar|X}} equals
Thus, Somers’ D equals
References
2. ^1 2 {{cite journal|last1=Newson|first1=Roger|title=Parameters behind "nonparametric" statistics: Kendall's tau, Somers' D and median differences|journal=Stata Journal|date=2002|volume=2|issue=1|pages=45–64| url=http://www.stata-journal.com/article.html?article=st0007}}
3. ^{{cite book |last1=O'Connell |first1=A. A.|year=2006|title=Logistic Regression Models for Ordinal Response Variables|publisher=SAGE Publications}}
- LGHS
- LGI
- LGIB
- LG ICC Cricket Rankings
- LG ICC cricket ratings
- LGIU
- LGK
- LG KE850
- LG KE970
- LG KG320
- LG KG800 (Chocolate)
- LGL
- L-glucuronate reductase
- L-glutamate
- L-glutamate oxidase
- L-Glutamic Acid
- L-glutamic acid decarboxylase
- L-glutamine
- L-Glutamine
- LG LX140
- L-glycol dehydrogenase
- LGM-1
- LGM 118
- LGM-118
- LGM118