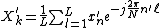“Sparse Fourier transform”的意思、由来-开放百科全书

The sparse Fourier transform (SFT) is a kind of discrete Fourier transform (DFT) for handling big data signals. Specifically, it is used in GPS synchronization, spectrum sensing and analog-to-digital converters.:^[1]

The fast Fourier transform (FFT) plays an indispensable role on many scientific domains, especially on signal processing. However, with the advent of big data era, the FFT still needs to be improved in order to save more computing power. Recently, the sparse Fourier transform (SFT) has gained a considerable amount of attention, for it performs well on analyzing the long sequence of data with few signal components.

Definition

Consider a sequence x_n of complex numbers. By Fourier series, x_n can be written as

Single frequency recovery

Assume only a single frequency exists in the sequence. In order to recover this frequency from the sequence, it is decent to utilize the relationship between adjacent points of the sequence.

Phase encoding

The phase k can be obtained by dividing the adjacent points of the sequence. In other words,

An aliasing-based search

Take

for an example. Now, we have three relatively prime integers 100, 101, and 103. Thus, the equation can be described as

Randomly binning frequencies

Now, we desire to explore the case of multiple frequencies, instead of a single frequency. The adjacent frequencies can be separated by the scaling c and modulation b properties. Namely, by randomly choosing the parameters of c and b, the distribution of all frequencies can be almost a uniform distribution. The figure Spread all frequencies reveals by randomly binning frequencies, we can utilize the single frequency recovery to seek the main components.

By randomly choosing c and b, the whole spectrum can be looked like uniform distribution. Then, taking them into filter banks can separate all frequencies, including Gaussians,^[3] indicator functions,^[4]^[5] spike trains,^[6]^[7]^[8]^[9] and Dolph-Chebyshev filters.^[10] Each bank only contains a single frequency.

The prototypical SFT

Identifying frequencies

By randomly bining frequencies, all components can be separated. Then, taking them into filter banks, so each band only contains a single frequency. It is convenient to use the methods we mentioned to recover this signal frequency.

Estimating coefficients

After identifying frequencies, we will have many frequency components. We can use Fourier transform to estimate their coefficients.

Repeating

Finally, repeating these two stages can we extract the most important components from the original signal.

Implementations

Further reading

References

1. ^¹{{cite journal |author1=Anna C. Gilbert |author2=Piotr Indyk |author3=Mark Iwen |author4=Ludwig Schmidt |title=Recent Developments in the Sparse Fourier Transform: A compressed Fourier transform for big data - IEEE Journals & Magazine |journal=ieeexplore.ieee.org |date=Sep 2014 |url=https://ieeexplore.ieee.org/document/6879613}}
2. ^{{cite journal |last1=Iwen |first1=M. A. |title=Combinatorial Sublinear-Time Fourier Algorithms |journal=Foundations of Computational Mathematics |date=2010-01-05 |volume=10 |issue=3 |pages=303–338 |doi=10.1007/s10208-009-9057-1}}
3. ^{{cite journal |author1=Haitham Hassanieh |author2=Piotr Indyk |author3=Dina Katabi |author4=Eric Price |title=Simple and Practical Algorithm for Sparse Fourier Transform |journal=epubs.siam.org |date=2012 |doi=10.1137/1.9781611973099.93 |url=https://epubs.siam.org/doi/abs/10.1137/1.9781611973099.93}}
4. ^{{cite journal |author1=A. C. Gilbert |others=S. Guha, P. Indyk, S. Muthukrishnan, M. Strauss |title=Near-optimal sparse fourier representations via sampling |journal=Proceeding STOC '02 Proceedings of the thiry-fourth annual ACM symposium on Theory of computing |date=2002 |pages=152-161 |doi=10.1145/509907.509933}}
5. ^{{cite journal |author1=A. C. Gilbert |author2=S. Muthukrishnan|author3= M. Strauss |title=Improved time bounds for near-optimal sparse Fourier representations |journal=Proc. SPIE, Wavelets XI |date=21 September 2005 |doi=10.1117/12.615931}}
6. ^{{cite journal |author1=Badih Ghazi |author2=Haitham Hassanieh|author3=Piotr Indyk|author4=Dina Katabi|author5=Eric Price|author6=Lixin Shi |title=Sample-optimal average-case sparse Fourier Transform in two dimensions - IEEE Conference Publication |journal=ieeexplore.ieee.org |url=https://ieeexplore.ieee.org/document/6736670}}
7. ^{{cite journal |last1=Iwen |first1=M. A. |title=Combinatorial Sublinear-Time Fourier Algorithms |journal=Foundations of Computational Mathematics |date=2010-01-05 |volume=10 |issue=3 |pages=303–338 |doi=10.1007/s10208-009-9057-1}}
8. ^{{cite journal |author1=Mark A.Iwen |title=Improved approximation guarantees for sublinear-time Fourier algorithms |journal=Applied and Computational Harmonic Analysis |date=2013-01-01 |volume=34 |issue=1 |pages=57–82 |doi=10.1016/j.acha.2012.03.007 |url=https://www.sciencedirect.com/science/article/pii/S1063520312000462?via%3Dihub |language=en |issn=1063-5203}}
9. ^{{cite journal |author1=Sameer Pawar |author2=Kannan Ramchandran |title=Computing a k-sparse n-length Discrete Fourier Transform using at most 4k samples and O(k log k) complexity - IEEE Conference Publication |journal=ieeexplore.ieee.org |date=2013 |url=https://ieeexplore.ieee.org/document/6620269}}
10. ^{{cite journal |last1=Hassanieh |first1=Haitham |last2=Indyk |first2=Piotr |last3=Katabi |first3=Dina |last4=Price |first4=Eric |title=Nearly Optimal Sparse Fourier Transform |journal=Proceedings of the Forty-fourth Annual ACM Symposium on Theory of Computing |date=2012 |pages=563–578 |doi=10.1145/2213977.2214029 |url=https://dl.acm.org/citation.cfm?id=2214029 |publisher=ACM}}