- Definition
- Estimation methods
- References
- Further reading
The spectral correlation density (SCD), sometimes also called the cyclic spectral density or spectral correlation function, is a function that describes the cross-spectral density of all pairs of frequency-shifted versions of a time-series. The spectral correlation density applies only to cyclostationary processes because stationary processes do not exhibit spectral correlation.[1] Spectral correlation has been used both in signal detection and signal classification.[2][3] The spectral correlation density is closely related to each of the bilinear time-frequency distributions, but is not considered one of Cohen's class of distributions.
Definition
The cyclic auto-correlation function of a time-series  is calculated as follows:
is calculated as follows:

where (*) denotes complex conjugation. By the Wiener–Khinchin theorem, the spectral correlation density is then:

Estimation methods
The SCD is estimated in the digital domain with an arbitrary resolution in frequency and time. There are several estimation methods currently used in practice to efficiently estimate the spectral correlation for use in real-time analysis of signals due to its high computational complexity. Some of the more popular ones are the FFT Accumulation Method (FAM) and the Strip-Spectral Correlation Algorithm.[4] One method to calculate the spectral correlation density of a discrete-time signal  with sample period
with sample period  is to first calculate the sliding window discrete Fourier transform:
is to first calculate the sliding window discrete Fourier transform:
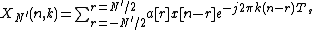 The variable N′ determines the frequency resolution of the spectral correlation density and the function
The variable N′ determines the frequency resolution of the spectral correlation density and the function 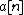 is a window function of choice. Then, the spectral correlation density is calculated:
is a window function of choice. Then, the spectral correlation density is calculated:
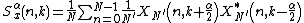
A fast-spectral-correlation (FSC) algorithm[5] has recently been introduced.
References
2. ^{{Cite journal|title = ATSC digital television signal detection with spectral correlation density|journal = Journal of Communications and Networks|date = 2014-12-01|issn = 1229-2370|pages = 600–612|volume = 16|issue = 6|doi = 10.1109/JCN.2014.000106|first = Do-Sik|last = Yoo|first2 = Jongtae|last2 = Lim|first3 = Min-Hong|last3 = Kang}}
3. ^{{Cite journal|title = Multi-User Signal Classification via Spectral Correlation|url = http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5421830|journal = 2010 7th IEEE Consumer Communications and Networking Conference (CCNC)|date = 2010-01-01|pages = 1–5|doi = 10.1109/CCNC.2010.5421830|first = S.|last = Hong|first2 = E.|last2 = Like|first3 = Zhiqiang|last3 = Wu|first4 = C.|last4 = Tekin|isbn = 978-1-4244-5175-3}}
4. ^{{Cite journal|title = Computationally efficient algorithms for cyclic spectral analysis|journal = IEEE Signal Processing Magazine|date = 1991-04-01|issn = 1053-5888|pages = 38–49|volume = 8|issue = 2|doi = 10.1109/79.81008|first = R.S.|last = Roberts|first2 = W.A.|last2 = Brown|first3 = H.H.|last3 = Loomis}}
5. ^{{Cite journal|last=Borghesani|first=P.|last2=Antoni|first2=J.|date=October 2018|title=A faster algorithm for the calculation of the fast spectral correlation|journal=Mechanical Systems and Signal Processing|volume=111|pages=113–118|doi=10.1016/j.ymssp.2018.03.059|issn=0888-3270}}
Further reading
- Napolitano, Antonio (2012-12-07). Generalizations of Cyclostationary Signal Processing: Spectral Analysis and Applications. John Wiley & Sons. {{ISBN|9781118437919}}.
- Pace, Phillip E. (2004-01-01). Detecting and Classifying Low Probability of Intercept Radar. Artech House. {{ISBN|9781580533225}}.
- 1963–64 Colchester United F.C. season
- 1963–64 Copa del Generalisimo
- 1963–64 Copa del Generalísimo
- 1963–64 Copa del Rey
- 1963–64 CPHL season
- 1963–64 Creighton Bluejays men's basketball team
- 1963–64 Czechoslovak Extraliga season
- 1963–64 Danish 1. division season
- 1963–64 DDR-Oberliga (ice hockey) season
- 1963–64 Detroit Pistons season
- 1963–64 Eintracht Frankfurt season
- 1963–64 European Cup (handball)
- 1963–64 European Cup (water polo)
- 1963–64 European Cup (women's handball)
- 1963–64 FA Cup qualifying rounds
- 1963–64 FC Dinamo Bucureşti season
- 1963–64 F.C. Inter Milan season
- 1963–64 F.C. Internazionale Milano season
- 1963–64 FC Lokomotiv Gorna Oryahovitsa season
- 1963–64 FIBA Women's European Champions Cup
- 1963–64 French Rugby Union Championship
- 1963–64 Fußball-Bundesliga
- 1963–64 Fußball-Regionalliga
- 1963–64 Galatasaray S.K. season
- 1963–64 Georgetown Hoyas men's basketball team