“Squire's theorem”的意思、由来-开放百科全书

词条

Squire's theorem

释义

References

In fluid dynamics, Squire's theorem states that of all the perturbations that may be applied to a shear flow (i.e. a velocity field of the form ), the perturbations which are least stable are two-dimensional, i.e. of the form 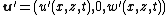than the three-dimensional disturbances^[1]. This applies to incompressible flows which are governed by the Navier–Stokes equations. The theorem is named after Herbert Squire, who proved the theorem in 1933^[2].

Squire's theorem allows many simplifications to be made in stability theory. If we want to decide whether a flow is unstable or not, it suffices to look at two-dimensional perturbations. These are governed by the Orr–Sommerfeld equation for viscous flow, and by Rayleigh's equation for inviscid flow.

References

1. ^Drazin, P. G., & Reid, W. H. (2004). Hydrodynamic stability. Cambridge university press.
2. ^Squire, H. B. (1933). On the stability for three-dimensional disturbances of viscous fluid flow between parallel walls. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 142(847), 621-628.

1 : Fluid dynamics

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。