- Structure of stable marriage with indifference
- References
Stable marriage with indifference is a variant of the stable marriage problem. Like in the original problem, the goal is to match all men to all women such that no pair of man and woman who are unmarried to each other, would simultaneously like to leave their present partners and pair with each other instead.
In the classic version of the problem, each person must rank the members of the opposite sex in strict order of preference. However, in a real-world setting, a person may prefer two or more persons as equally favorable partner. Such tied preference is termed as indifference.
Below is such an instance where 
finds tie between 
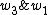and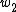 
finds tie between 
.
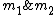If tied preference lists are allowed then the stable marriage problem will have three notions of stability which are discussed in the below sections.
1. A matching is called weakly stable unless there is a couple each of whom strictly prefers the other to his/her partner in the matching. Robert W. Irving[1] has extended the Gale–Shapley algorithm as below to provide such weakly stable matching in 
time where n is size of stable marriage problem. Ties in men and women's preference list are broken arbitrarily. Preference lists are reduced as algorithm proceeds.
Assign each person to be free;
while (some man m is free) do
begin
w := first woman on m’s list;
m proposes, and becomes engaged, to w;
if (some man m' is engaged to w) then
assign m' to be free;
for each (successor m of m on w’s list) do
delete the pair (m, w)
end;
output the engaged pairs, which form a stable matching
2. A matching is called super-stable if there is no couple each of whom either strictly prefers the other to his/her partner or is indifferent between them. Robert W. Irving[1] has modified the above algorithm to check whether such super stable matching exists and outputs matching in time if it exists. Below is the pseudo-code.assign each person to be free;
repeat
while (some man m is free) do
for each (woman w at the head of m’s list) do
begin
m proposes, and becomes engaged, to w;
for each (strict successor m' of m on w’s list) do
begin
if (m' is engaged) to w then
break the engagement;
delete the pair (m'. w)
end
end
for each (woman w who is multiply engaged) do
begin
break all engagements involving W;
for each (man m at the tail of w’s list) do
delete the pair (m. w)
until (some man’s list is empty) or (everyone is engaged);
if everyone is engaged then
the engagement relation is a super-stable matching
else
no super-stable matching exists
time which is explained in the Lemma 4.6 of .[1]Assign each person to be free;
repeat
while (some man m is free) do
for each (woman w at the head of m's list) do
begin
m proposes, and becomes engaged, to w;
for each (strict successor m' of m on w’s list) do
begin
if (m' is engaged) to w then
break the engagement;
delete the pair (m'. w)
end
end
if (the engagement relation does not contain a perfect matching) then begin
find the critical set Z of men;
for each (woman w who is engaged to a man in Z) do
begin
break all engagements involving w;
delete the pair (m, w)
end;
until (some man’s list is empty) or (everyone is engaged);
if everyone is engaged then
the engagement relation is a super-stable matching
else
no strongly stable matching exists
Structure of stable marriage with indifference
In many problems, there can be several different stable matchings. The set of stable matchings has a special structure. David F. Manlove[2] proved that, both the set of strong stable matchings and the set of super stable matchings form a distributive lattice.
References
2. ^{{Cite journal|last=Manlove|first=David F.|date=2002-10-15|title=The structure of stable marriage with indifference|url=http://www.sciencedirect.com/science/article/pii/S0166218X01003225|journal=Discrete Applied Mathematics|volume=122|issue=1|pages=167–181|doi=10.1016/S0166-218X(01)00322-5|issn=0166-218X}}
- 1980 North Carolina Tar Heels football season
- 1980 North Dakota gubernatorial election
- 1980 North-East Fife District Council election
- 1980 Northern Illinois Huskies football
- 1980 Northern Illinois Huskies football season
- 1980 Northwestern Wildcats football
- 1980 Northwestern Wildcats football season
- 1980 Northwestern Wildcats football team
- 1980 Norwegian First Division
- 1980 Notre Dame Fighting Irish football
- 1980 Notre Dame Fighting Irish football season
- 1980 (number)
- 1980 Oakland Athletics
- 1980 Oakland Raiders
- 1980 Oakland Raiders football
- 1980 Oakland Raiders football team
- 1980 Ohio Bobcats football
- 1980 Ohio Bobcats football season
- 1980 Ohio Bobcats football team
- 1980 Ohio State Buckeyes football
- 1980 Ohio State Buckeyes football season
- 1980 Oklahoma Sooners football
- 1980 Oklahoma Sooners football season
- 1980 Oklahoma State Cowboys football team
- 1980 Oktoberfest bombing