“Strictly-Correlated-Electrons density functional theory”的意思、由来-开放百科全书

词条

Strictly-Correlated-Electrons density functional theory

释义

The Strictly-Correlated-Electron reference system
Calculation of the co-motion functions and interaction energy of the SCE system
Combining the strictly-correlated-electron and the Kohn-Sham approaches
References

The Strictly-Correlated-Electrons (SCE) density functional theory (SCE DFT) approach, originally proposed by Michael Seidl [1], is a formulation

of density functional theory, alternative to the widely used Kohn-Sham DFT, especially aimed at the study of

strongly-correlated systems. The essential difference between the two approaches is the choice of the auxiliary system (having the same density

as the real, physical one). In Kohn-Sham DFT this system is composed by non-interacting electrons, for which the kinetic energy can be calculated

exactly and the interaction term has to be approximated. In SCE DFT, instead, the starting point is totally the opposite one: the auxiliary system has infinite electronic

correlation and zero kinetic energy.

The Strictly-Correlated-Electron reference system

To understand how the SCE system is constructed, it is useful to first think in terms of a simple example. Consider a collection of identical classical charges

(with repulsive Coulomb interaction) confined in some container with a given shape. If let alone, the charges will distribute themselves within the container until they reach

the spatial configuration that minimizes their interaction energy (in equilibrium, their kinetic energy is zero). Of course, the equilibrium position of the charges will

depend on the shape of the container.

Suppose now that in this classical system one of the charges, which we can label as number “1”, is pinned at some arbitrary position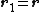

inside the container. Clearly, the equilibrium position of the other 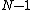charges will now not only depend on the shape of the container, but also on the position

of the pinned charge. Thus, for a given confining geometry, one can write the position of the -th particle ,

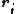, as a function of : .

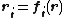In the SCE system, as in the classical example described above, the position 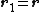of a reference electron determines the position of the remaining

ones. The analogue role of the confining container is now played by the condition that the density at each point must be the same as that of the real system,

: the electrons will always try to be as far apart from each other as possible, in order to minimize their repulsion, but always restricted

by this condition. The positions 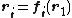are called co-motion functions and play a fundamental role in the SCE formalism, analogue to

the one of the Kohn-Sham single-particle orbitals in Kohn-Sham DFT [2-4].

Calculation of the co-motion functions and interaction energy of the SCE system

For a given density , the probability of finding one electron at a certain position is the same as that of finding

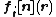the -th electron at , or, equivalently,

The co-motion functions can be obtained from the integration of this equation. An analytical solution exists for 1D systems [2,3], but not for the general case.

The interaction energy of the SCE system for a given density can be exactly calculated in terms of the co-motion functions as [6]

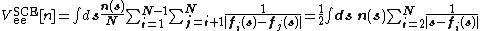Notice that this is analogous to the Kohn-Sham approach, where the non-interacting kinetic energy is expressed in terms of the Kohn-Sham single-particle orbitals.

A very important property of the SCE system is the following one: since the position of one particle determines the position of the remaining ones, the total

coulomb repulsion felt by a particle at a point becomes a function of only itself. This force can then be written

as minus the gradient of some one-particle potential [5,6]:

At the same time, it can be shown that the potential satisfies the relation [4,6]

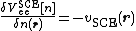A promising route towards the application of the SCE approach to systems with general symmetry is the mass-transportation-theory reformulation of the approach [8]. This is

based on the analogies between the SCE problem and the dual Kantorovich problem [8]. The SCE wave function is also very useful

to set rigorous bounds for the constant appearing in the Lieb-Oxford inequality.

Combining the strictly-correlated-electron and the Kohn-Sham approaches

The one-body potential can be used to approximate the Hartree-exchange-correlation (Hxc) potential of the Kohn-Sham DFT approach [4,5].

Indeed, one can see the analogy between the expression relating the functional derivative of and and

the well-known one of Kohn-Sham DFT

which relates the Hartree-exchange-correlation (Hxc) functional and the corresponding potential.

The approximation (which becomes exact in the limit of infinitely strong interaction [5]) corresponds to writing the Hohenberg-Kohn functional as

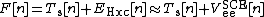where 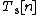is the non-interacting kinetic energy.

One has therefore 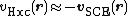and this leads to the Kohn-Sham equations

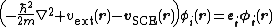which can be solved self-consistently.

Since the potential is constructed from the exact properties of the SCE system [2-4], it is able to capture the effects of the

strongly-correlated regime, as it has been recently shown in the first applications of this "KS-SCE DFT" approach to simple model systems [5-7]. In particular, the

method has allowed to observe Wigner localization in strongly-correlated electronic systems without introducing any artificial symmetry breaking [5-7].

References

1.M. Seidl, Strong-interaction limit of density-functional theory, Phys. Rev. A 60, 4387 (1999); Michael Seidl, John P. Perdew, and Mel Levy,

Strictly correlated electrons in density-functional theory, Phys. Rev. A 59, 51 (1999).

2.M. Seidl, P. Gori-Giorgi, and A. Savin, Strictly correlated electrons in density functional theory: A general formulation with applications to spherical densities,

Phys. Rev. A 75, 042511 (2007).

3.P. Gori-Giorgi and M. Seidl, Density functional theory for strongly-interacting electrons: Perspectives for Physics and Chemistry,

Phys. Chem. Chem. Phys. 12, 14405 (2010).

4.P. Gori-Giorgi, M. Seidl, and G. Vignale, Density functional theory for strongly interacting electrons, Phys. Rev. Lett., 103, 166402 (2009).

5.F. Malet and P. Gori-Giorgi, Strong correlation in Kohn-Sham density functional theory, Phys. Rev. Lett. 109, 246402 (2012).

6.F. Malet, A. Mirtschink, J. C. Cremon, S. M. Reimann, and P. Gori-Giorgi, Kohn-Sham density functional theory for quantum wires in arbitrary correlation regimes,

Phys. Rev. B 87, 115146 (2013).

7.C. B. Mendl, F. Malet, and P. Gori-Giorgi, Wigner localization in quantum dots from Kohn-Sham density functional theory without symmetry breaking,

Phys. Rev. B 89, 125106 (2014).

8.G. Buttazzo, L. De Pascale, and P. Gori-Giorgi, Optimal-transport formulation of electronic density-functional theory, Phys. Rev. A 85, 062502 (2012);

C. Cotar, G. Friesecke, and C. Klüppelberg, Density Functional Theory and Optimal Transportation with Coulomb Cost, Comm. Pure Appl. Math. 66, 548 (2013).

1 : Density functional theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。