“System U”的意思、由来-开放百科全书

词条

System U

释义

Formal definition
Girard's paradox
References
Further reading

In mathematical logic, System U and System U⁻ are pure type systems, i.e. special forms of a typed lambda calculus with an arbitrary number of sorts, axioms and rules (or dependencies between the sorts). They were both proved inconsistent by Jean-Yves Girard in 1972.^[1] This result led to the realization that Martin-Löf's original 1971 type theory was inconsistent as it allowed the same "Type in Type" behaviour that Girard's paradox exploits.

Formal definition

System U is defined^[2]{{rp|352}} as a pure type system with

three sorts ;
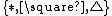two axioms 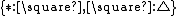; and
five rules .

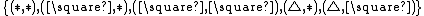System U⁻ is defined the same with the exception of th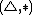e rule.

The sorts and are conventionally called “Type” and “Kind”, respectively; the sort doesn't have a specific name. The two axioms describe the containment of types in kinds (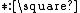) and kinds in (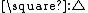). Intuitively, the sorts describe a hierarchy in the nature of the terms.

All values have a type, such as a base type (e.g. is read as “{{math|b}} is a boolean”) or a (dependent) function type (e.g. 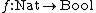is read as “{{math|f}} is a function from natural numbers to booleans”).
is the sort of all such types (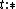 is read as “{{math|t}} is a type”). From we can build more terms, such as which is the kind of unary type-level operators (e.g. 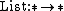is read as “{{math|List}} is a function from types to types”, that is, a polymorphic type). The rules restrict how we can form new kinds.
is the sort of all such kinds (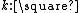 is read as “{{math|k}} is a kind”). Similarly we can build related terms, according to what the rules allow.
is the sort of all such terms.

The rules govern the dependencies between the sorts: says that values may depend on values (functions), 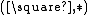allows values to depend on types (polymorphism), allows types to depend on types (type operators), and so on.

Girard's paradox

The definitions of System U and U⁻ allow the assignment of polymorphic kinds to generic constructors in analogy to polymorphic types of terms in classical polymorphic lambda calculi, such as System F. An example of such a generic constructor might be{{r|SoerensenUrzyczyn2006|page=353}} (where k denotes a kind variable)

.

This mechanism is sufficient to construct a term with the type , which implies that every type is inhabited. By the Curry–Howard correspondence, this is equivalent to all logical propositions being provable, which makes the system inconsistent.

Girard's paradox is the type-theoretic analogue of Russell's paradox in set theory.

References

1. ^{{cite paper |first=Jean-Yves |last=Girard |title=Interprétation fonctionnelle et Élimination des coupure de l'arithmétique d'ordre supérieur |year=1972 |url=https://www.cs.cmu.edu/~kw/scans/girard72thesis.pdf }}
2. ^{{cite book |first=Morten Heine |last=Sørensen |first2=Paweł |last2=Urzyczyn |title=Lectures on the Curry–Howard isomorphism |location= |publisher=Elsevier |year=2006 |isbn=0-444-52077-5 |chapter=Pure type systems and the lambda cube }}

Formal definition

Girard's paradox

References

Further reading