- Description
- References
Two-step M-estimators deals with M-estimation problems that require preliminary estimation to obtain the parameter of interest. Two-step M-estimation is different from usual M-estimation problem because asymptotic distribution of the second-step estimator generally depends on the first-step estimator. Accounting for this change in asymptotic distribution is important for valid inference.
Description
The class of two-step M-estimators includes Heckman's sample selection estimator,[1] weighted non-linear least squares, and ordinary least squares with generated regressors.[2]
To fix idea, let 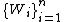
 be an i.i.d. sample.
be an i.i.d. sample.  and
and  are subsets of Euclidean spaces
are subsets of Euclidean spaces  and
and  , respectively. Given a function
, respectively. Given a function 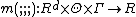 , two-step M-estimator
, two-step M-estimator  is defined as:
is defined as:

where  is a parameter that needs to be estimated in the first step.
is a parameter that needs to be estimated in the first step.
Consistency of two-step M-estimators can be verified by checking consistency conditions for usual M-estimators, although some modification might be necessary. In practice, the important condition to check is identification condition.[2] If 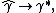 where
where 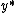 where
where 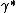 is a non-random vector, then the identification condition is that
is a non-random vector, then the identification condition is that  has a unique maximizer over
has a unique maximizer over  .
.
Under regularity conditions, two-step M-estimators have asymptotic normality. An important point to note is that asymptotic variance of a two-step M-estimator is generally not the same as that of the usual M-estimator in which the first step estimation is not necessary.[3] This fact is intuitive because 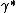 is a random object and its variability should influence the estimation of
is a random object and its variability should influence the estimation of  . However, there exists a special case in which the asymptotic variance of two-step M-estimator takes the form as if there were no first-step estimation procedure. Such special case occurs if:
. However, there exists a special case in which the asymptotic variance of two-step M-estimator takes the form as if there were no first-step estimation procedure. Such special case occurs if:
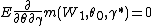
where  is the true value of
is the true value of  and
and 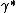 is the probability limit of
is the probability limit of  .[3] To interpret this condition, first note that under regularity conditions,
.[3] To interpret this condition, first note that under regularity conditions, 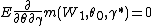 since
since  is the maximizer of
is the maximizer of 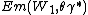 . So the condition above implies that small perturbation in γ has no impact on the First-Order condition. Thus, in large sample, variability of
. So the condition above implies that small perturbation in γ has no impact on the First-Order condition. Thus, in large sample, variability of  does not affect the argmax of the objective function, which explains invariant property of asymptotic variance. Of course, this result is valid only as the sample size tends to infinity, so the finite-sample property could be quite different.
does not affect the argmax of the objective function, which explains invariant property of asymptotic variance. Of course, this result is valid only as the sample size tends to infinity, so the finite-sample property could be quite different.
References
2. ^1 Wooldridge, J.M., Econometric Analysis of Cross Section and Panel Data, MIT Press, Cambridge, Mass.
3. ^1 Newey, K.W. and D. McFadden, Large Sample Estimation and Hypothesis Testing, in R. Engel and D. McFadden, eds., Handbook of Econometrics, Vol.4, Amsterdam: North-Holland.
- Yamaha XT200
- Yamaha XT250
- Yamaha XT 500
- Yamaha XT 600
- Yamaha XTZ 250
- Yamaha (yacht)
- Yamaha YD1
- Yamaha YD 100
- Yamaha YM2610B
- Yamaha YMF292
- Yamaha YQ50 Aerox R
- Yamaha YS200
- Yamaha YZF-R3
- Yam Ah Mee
- Yamahoko
- Yamaho Yama
- Yamai
- Yama-Ichi War
- Yamai language
- Yama in Buddhist and Chinese mythology
- Yamaji
- Yamajijii
- Yama-jijii
- Yamaji Motoharu
- YamaJo