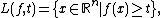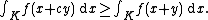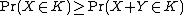“Anderson's theorem”的意思、由来-开放百科全书

词条

Anderson's theorem

释义

Statement of the theorem
Application to probability theory
References

{{about|Anderson's theorem in mathematics|the Anderson orthogonality theorem in physics|Anderson orthogonality theorem}}

In mathematics, Anderson's theorem is a result in real analysis and geometry which says that the integral of an integrable, symmetric, unimodal, non-negative function f over an n-dimensional convex body K does not decrease if K is translated inwards towards the origin. This is a natural statement, since the graph of f can be thought of as a hill with a single peak over the origin; however, for n ≥ 2, the proof is not entirely obvious, as there may be points x of the body K where the value f(x) is larger than at the corresponding translate of x.

Anderson's theorem also has an interesting application to probability theory.

Statement of the theorem

Let K be a convex body in n-dimensional Euclidean space Rⁿ that is symmetric with respect to reflection in the origin, i.e. K = −K. Let f : Rⁿ → R be a non-negative, symmetric, globally integrable function; i.e.

f(x) ≥ 0 for all x ∈ Rⁿ;
f(x) = f(−x) for all x ∈ Rⁿ;

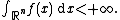
Suppose also that the super-level sets L(f, t) of f, defined by

are convex subsets of Rⁿ for every t ≥ 0. (This property is sometimes referred to as being unimodal.) Then, for any 0 ≤ c ≤ 1 and y ∈ Rⁿ,

Application to probability theory

Given a probability space (Ω, Σ, Pr), suppose that X : Ω → Rⁿ is an Rⁿ-valued random variable with probability density function f : Rⁿ → [0, +∞) and that Y : Ω → Rⁿ is an independent random variable. The probability density functions of many well-known probability distributions are p-concave for some p, and hence unimodal. If they are also symmetric (e.g. the Laplace and normal distributions), then Anderson's theorem applies, in which case

for any origin-symmetric convex body K ⊆ Rⁿ.

References

{{cite journal | last=Gardner | first=Richard J. | title=The Brunn-Minkowski inequality | journal=Bull. Amer. Math. Soc. (N.S.) | volume=39 | issue=3 | year=2002 | pages=355–405 (electronic) | doi=10.1090/S0273-0979-02-00941-2 }}

3 : Theorems in geometry|Probability theorems|Theorems in real analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。