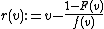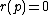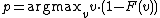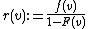“Virtual valuation”的意思、由来-开放百科全书

词条

Virtual valuation

释义

Applications
Examples
Regularity
See also
References

In auction theory, particularly Bayesian-optimal mechanism design, a virtual valuation of an agent is a function that measures the surplus that can be extracted from that agent.

A typical application is a seller who wants to sell an item to a potential buyer and wants to decide on the optimal price. The optimal price depends on the valuation of the buyer to the item, . The seller does not know exactly, but he assumes that is a random variable, with some cumulative distribution function 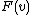and probability distribution function .

The virtual valuation of the agent is defined as:

Applications

A key theorem of Myerson^[1] says that:

The expected profit of any truthful mechanism is equal to its expected virtual surplus.

In the case of a single buyer, this implies that the price should be determined according to the equation:

This guarantees that the buyer will buy the item, if and only if his virtual-valuation is weakly-positive, so the seller will have a weakly-positive expected profit.

This exactly equals the optimal sale price – the price that maximizes the expected value of the seller's profit, given the distribution of valuations:

Virtual valuations can be used to construct Bayesian-optimal mechanisms also when there are multiple buyers, or different item-types.^[2]

Examples

1. The buyer's valuation has a continuous uniform distribution in . So:

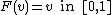
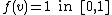
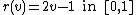
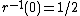, so the optimal single-item price is 1/2.

2. The buyer's valuation has a normal distribution with mean 0 and standard deviation 1. 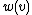is monotonically increasing, and crosses the x-axis in about 0.75, so this is the optimal price. The crossing point moves right when the standard deviation is larger.^[3]

Regularity

A probability distribution function is called regular if its virtual-valuation function is weakly-increasing. Regularity is important because it implies that the virtual-surplus can be maximized by a truthful mechanism.

A sufficient condition for regularity is monotone hazard rate, which means that the following function is weakly-increasing:

Monotone-hazard-rate implies regularity, but the opposite is not true.

References

1. ^{{cite journal|doi = 10.1287/moor.6.1.58|title = Optimal Auction Design|journal = Mathematics of Operations Research|volume = 6|pages = 58|year = 1981|last1 = Myerson|first1 = Roger B.}}
2. ^{{cite conference|doi=10.1145/1250910.1250946|chapter=Algorithmic pricing via virtual valuations|title=Proceedings of the 8th ACM conference on Electronic commerce – EC '07|pages=243|year=2007|last1=Chawla|first1=Shuchi|last2=Hartline|first2=Jason D.|last3=Kleinberg|first3=Robert|isbn=9781595936530|arxiv=0808.1671}}
3. ^See this [https://www.desmos.com/calculator/6bki0d0wqi Desmos graph].

1 : Mechanism design

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Applications

Examples

Regularity

See also

References